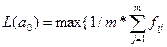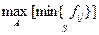Критерий Лапласа

Этот критерий основывается на известном принципе недостаточного обоснования Бернулли- Лапласа (впервые был сформулирован Я.Бернулли). Поскольку вероятности ситуаций не известны, информация, необходимая для вывода о том, что эти вероятности различны, отсутствует (в противном случае эти вероятности можно было бы определить и задачу уже не следовало бы рассматривать как задачу принятия решений в условиях неопределенности)

В соответствии с принципом «недостаточного обоснования» тогда, когда нет оснований считать, что одно из состояний среды из S более вероятным, чем любое другое состояние, их следует считать равновероятными, т.е. вероятности всех состояний оцениваются величиной:

Pj=1/m (j=1,...,m)

где m - число элементов множества S возможных ситуаций.

Таким образом, задача принятия решений в условиях неопределенности сводится к задаче принятия в условиях риска. При этом выбирается решение, дающее наибольший ожидаемый выигрыш при предположении равной вероятности всех ситуаций, т.е. оптимальным считается такое решение а_о,для которого

где 1/m - вероятности состояний s_j, j=1,...,m, определенные в соответствии с принципом «недостаточного обоснования».

Для рассматриваемого примера L(a) будет следующим:

 

Таблица 13 - Результаты расчетов

ai\sj	S1	S2	S3	S4	L(ai)
a1			-12000	-21000
a2
a3					69562,5
a4					86437,5
a5					90937,5

 

L (a₁) = 1/4*(15000+37500-12000-21000) = 4875;

L (a₂)= 1/4*(52500+75000+25500+16500)= 42375 и т.д.

Оптимальным по критерию Лапласа является решение а₅.

Критерий Вальда (критерий «крайнего пессимизма»)

Этот критерий является наиболее «осторожным»: ЛПР исходит из того, что наступит «наихудшая» ситуация и выбирает «наилучшую из наихудших» возможностей. Если ОФ выражает «выигрыш» ЛПР, то выбирается решение, дающее

Если ОФ выражает потери ЛПР, решение выбирается исходя из условия

В рассматриваем примере ОФ выражает «выигрыш».

 

Таблица 14 - ОФ F⁺(выражает выигрыши)

ai\sj	S1	S2	S3	S4	V(a)
a1			-12000	-21000	-21000
a2				16500,0
a3		71250,0
a4
a5

 

Оптимальным по критерию Вальда является решение a₄, которое в «наихудшей» ситуации S2 обеспечивает получение выигрыша 67500.