Модели исследования операций (Транспортная задача)
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления А1, А2, …, Аm в n пунктов назначения В1, В2, …, Вn. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим Сij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через Аi – запасы груза в i-ом пункте отправления, через bj – потребности в грузе в j-ом пункте назначения, а через Хij – количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка зачади состоит в определении минимального значения функции при условиях Поскольку переменные Очевидно, общее наличие груза у поставщиков равно то модель такой транспортной задачи называется закрытой. В противном случае – открытой. В случае превышения запаса над потребностью, т.е. Вводится фиктивный (n+1) потребитель (или пункт назначения) с потребностью равной:
А соответствующие транспортные тарифы от всех поставщиков до фиктивного потребителя полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (5). В случае превышения потребности некоторого потребителя над общими запасами, т.е. Вводится фиктивный (m+1) пункт отправления с запасом груза в нем, равным с потребностью равной:
А соответствующие транспортные тарифы от фиктивного поставщика до всех потребителей полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (5). Рассмотрим конкретную задачу: Условие: Четыре предприятия Новгородской области (ООО «Старорусский хлеб, ИП Смородин, Старорусское РАЙПО и ООО «Пекарь») для производства продукции получают сырье от трех поставщиков. Потребности в сырье каждого из предприятий соответственно равны 900, 600, 800 и 600 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 600, 800 и 1000 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей: Составить такой план перевозок, при котором общая стоимость перевозок является минимальной. Обозначим через Хij количество единиц сырья, перевозимого из i-го пункта его получения на j-е предприятие. Задача является открытой, так как сумма запасов грузов 600 + 800 + 1000 = 2400 в местах отправления, не равна сумме потребностей грузов в местах назначения 900 + 600 + 800 + 600 = 2900. Так как потребности в грузах превышают их запасы, то вводим фиктивного поставщика (Поставщик 4), у которого запас груза равен 2900 – 2400 = 500. В этом случае общий запас станет равным 2900 и мы получим закрытую транспортную задачу. При этом все тарифы от фиктивного поставщика ко всем потребителям груза полагаются равными нулю. В матрице тарифов появится четвертая строка, в которой стоят все нули. Целевая функция не изменится. Условия доставки и вывоза необходимого и имеющегося сырья обеспечиваются за счет выполнения следующих равенств: Х11 + Х12 + Х13 + Х14 = 600 (6) Х21 + Х22 + Х23 + Х24 = 800 (7) Х31 + Х32 + Х33 + Х34 = 1000 (8) Х41 + Х42 + Х43 + Х44 = 500 (9)
Х11 + Х21 + Х31 + Х41 = 900 (10) Х12 + Х22 + Х32 + Х42 = 600 (11) Х13 + Х23 + Х33 + Х43 = 800 (12) Х14 + Х24 + Х34 + Х44 = 600 (13) При данном плане перевозок F = 4x11 + 3x12 + 213 + 1x14 + 2x21 + 1x22 + 7x23 + 9x24 + 3x31 + 6x32 + 8x33 + 4x34 → min Таким образом, математическая постановка задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений (6) – (13), при котором целевая функция принимает минимальное значение. Для решения этой задачи средствами Microsoft Excel необходимо использовать опцию «Поиск решения». Все расчеты в формульном виде в Приложении Б.
Таблица 1 - Информация о поставщиках и покупателях
Таблица 2 - Матрица затрат на перевозку
Задав ограничения и использовав для нахождения решения «Поиск решения», получаем, что минимальные затраты на перевозку грузов будут равны 5200 рублей.
|

 (1)
(1)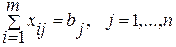 (2)
(2) (3)
(3)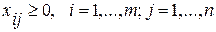 (4)
(4)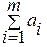 , а общая потребность в грузе в пунктах назначения равна
, а общая потребность в грузе в пунктах назначения равна 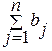 единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.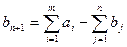
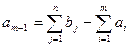
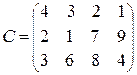
 , общая стоимость перевозок составит:
, общая стоимость перевозок составит:


