Линию пересечения призмы с плоскостью можно построить, путем нахождения точек пересечения ее ребер с данной плоскостью или определяя линии пересечения отдельных граней призмы с плоскостью.
В результате пересечения поверхности призмы плоскостью может быть получен прямоугольник (рис.6а), если эта плоскость параллельна боковым ребрам призмы, или различного вида многоугольники (рис.6б, в), если плоскость не параллельна им.
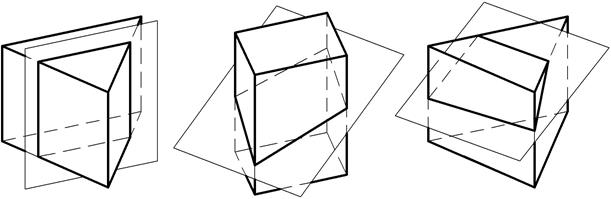а) б) в)
|
| Рис.6. Пересечение призмы плоскостью
|
На рис.7 показаны ортогональные проекции призмы, рассеченной фронтально проецирующей плоскостью α (задана своим фронтальным следом foα;).В сечении получен четырехугольник ABCD, фронтальная проекция A"B"C"D" которого принадлежит foα;.
Точки А, В являются точками пересечения боковых ребер призмы с плоскостью α, а отрезок CD – линия пересечения верхнего основания призмы с этой плоскостью. Плоскость α считается прозрачной.
Натуральный вид сечения ABCD построен способом замены плоскостей проекций, для чего введена новая плоскость проекций, параллельная плоскости α, и на эту плоскость ортогонально спроецированы точки А, В, С, D. Из проекций А", В", С", D" направлены линии связи, перпендикулярные к следу foα, и на свободном поле чертежа проведена линия AD, параллельная foα. Эта линия принята за базу отсчета размеров Y на фигуре сечения потому, что прямая AD принадлежит фронтальной плоскости задней грани призмы, которую принимают за базовую. Точки В и С построены с помощью размеров YВ и ХС.
|
| Рис.7. Пересечение призмы фронтально-проецирующей плоскостью
|
