НАКЛОННОГО СЕЧЕНИЯ МОДЕЛИ

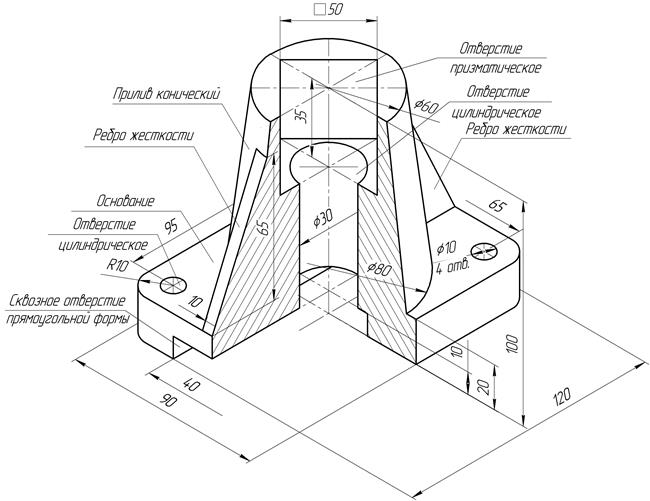
Пример 1. Рассмотрим построение наклонного сечения модели, изображенной на рис.2.

Рис.2. Изображение модели в прямоугольной изометрии

 

На рис.3 приведено изображение той же модели, но в ортогональных проекциях с обозначением плоскости сечения (А-А).

Рис.3. Изображение модели в ортогональных проекциях

 

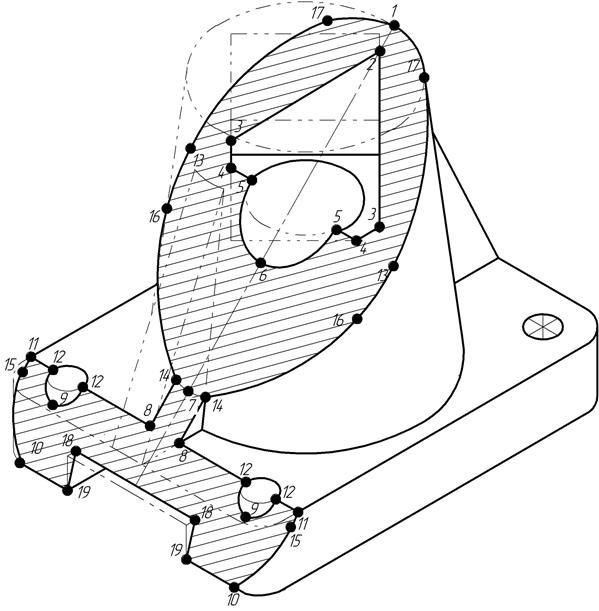
Анализируя положение секущей плоскости замечаем, что в данном случае в неё попадают (рис.4): конический прилив (точки 1, 7, 13, 14, 16, 17); призматическое отверстие (точки 2, 3, 4); цилиндрическое отверстие диаметром 30мм (точки 5, 6); ребро жесткости (точки 7, 8); основание прямоугольной формы со скругленными краями (точки 10, 11, 15); два цилиндрических отверстия диаметром 10мм каждое (точки 9, 12); сквозное отверстие прямоугольной формы (точки 18, 19).

От пересечения призматических отверстий, ребра жесткости и призматической части основания секущей плоскостью в сечении получаются прямоугольники. От пересечения конического прилива, цилиндрических отверстий, закругленной части основания – эллипсы.

Рис.4. Сечение модели наклонной плоскостью в прямоугольной изометрии

 

На фронтальной проекции модели обозначаем все точки, в которых линия сечения А-А пересекает очерковые образующие наружных и внутренних поверхностей модели, а также осевые линии (точки1"…19").

Затем находим горизонтальные проекции 1'…19' отмеченных на фронтальной проекции точек, используя линии связи и принадлежность их соответствующим геометрическим телам.

Так как заданная модель имеет ось симметрии, то фигура сечения будет также симметрична. Ось симметрии фигуры сечения 1 - 19 будет параллельна секущей плоскости.

Далее на свободном поле чертежа проводим ось симметрии сечения 1 - 19 параллельно линии сечения А-А и на ней откладываем расстояния, равные расстояниям между фронтальными проекциями 1"…19" точек.

Затем проводим линии, перпендикулярные к оси симметрии 1 - 19. На этих линиях находим положение каждой отмеченной точки для наружного и внутреннего контуров модели. При этом положение каждой точки определяется расстоянием ее горизонтальной проекции от осевой линии изображения – на горизонтальной проекции модели.

Например, расстояние 6-16 равно расстоянию 6'…16'. Длина большой оси эллипса 1 - 7, получающегося при пересечении конического прилива секущей плоскостью, равна расстоянию 1" - 7". А длина малой оси этого эллипса 13 - 13 равна расстоянию 13' - 13'.

Соединяем построенные точки с учетом формы линии сечения.

Далее заштриховываем сечение и выполняем надпись А-А.

Затем проверяем правильность выполненного сечения и обводим его контур линиями требуемой толщины (рис.5).

 

 

Рис.5. Чертеж модели с выполненным наклонным сечением

 

Пример 2. На рис.7 приведен пример построения наклонного сечения модели, не имеющей оси симметрии. В этом случае для построения использованы новые координатные оси Х₁ и Y₁ , лежащие в секущей плоскости. Ось Х₁ параллельна плоскости π₂, ось Y₁ перпендикулярна плоскости π₂. Координаты точек сечения по оси Х₁ равны координатам по оси Х₁ их фронтальных проекций. Координаты точек сечения по оси Y₁ равны координатам по этой оси их горизонтальных проекций.

Рис.7 Изображение наклонного сечения модели, не имеющей оси симметрии