Любая плоскость пересекает сферу по окружности. Если секущая плоскость параллельна плоскости проекций, окружность сечения проецируется на эту плоскость проекций без искажения. Если же плоскость не параллельна ни одной из плоскостей проекций, проекциями окружности являются эллипсы. Большая ось этих эллипсов равна диаметру окружности сечения (большой осью эллипса является тот диаметр окружности сечения, который параллелен плоскости проекций). Величина малых осей эллипсов зависит от угла наклона секущей плоскости к плоскостям проекций.
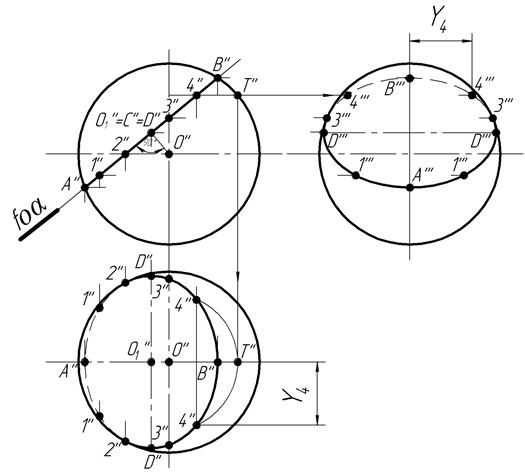
На рис.14 изображена сфера, рассеченная фронтально проецирующей плоскостью α (задана своим фронтальным следом foα;).Эта плоскость пересекает сферу по окружности диаметра АВ = А" В" с центром в точке О1 (проекция О1" – точка пересечения foα с перпендикуляром, опущенным из проекции О" центра сферы на плоскость α;).Горизонтальная и профильная проекции этой окружности представляют собой эллипсы, которые можно построить по их большой и малой осям: А'В', C'D' и А"'В"', C"'D"', где C'D' = С "' D "'= А"В". Точки А, В линии сечения принадлежат главному фронтальному меридиану, точки 2 – экватору, точки 3 – главному профильному меридиану. Случайная точка линии сечения может быть построена с помощью параллели сферы (например, точка 4).
|
| Рис.14. Пересечение шара фронтально-проецирующей плоскостью
|





