Сечение цилиндра проецирующей плоскостью

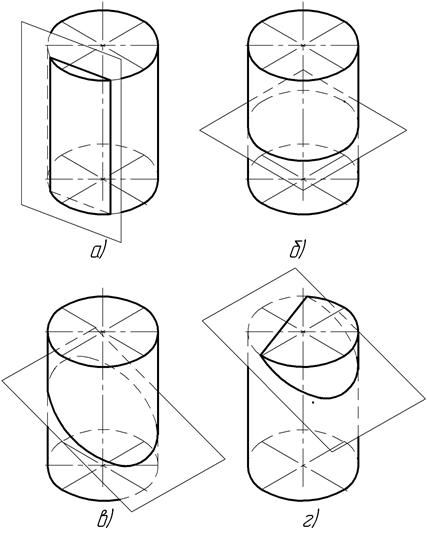
При пересечении цилиндра плоскостью фигура сечения зависит от угла наклона плос­кости по отношению к образующим цилиндра.

Если плоскость парал­лельна образующим (рис.9а ), в сечении цилиндра получается прямоугольник, если перпендикулярна (рис.9б) - окружность, если плоскость наклонена к образующим, т. е. составляет с ними угол, отличный от 0 и 90^о, в сечении цилиндра получается эллипс (рис.9в ) или часть его (рис.9г ).

Рис.9. Пересечение цилиндра плоскостью

 

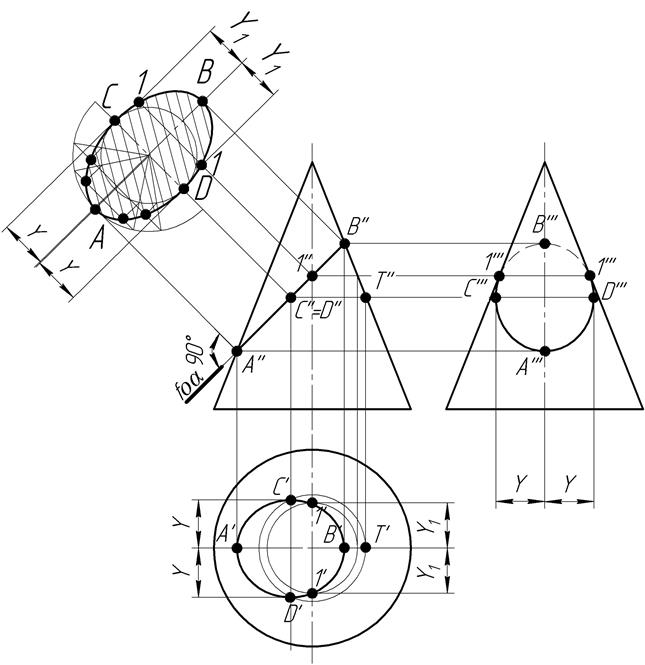
На рис. 10 изображен цилиндр, рассеченный фронтально прое­цирующей плоскостью α (задана своим фронтальным следом foα;).

Линией пересечения является эллипс. Большая ось эллипса – АВ=А"В", малая ось CD = С'D' – диа­метр цилиндра. Натуральный вид сечения построен способом заме­ны плоскостей проекций. Ось симметрии А₀В₀ (большая ось эл­липса) параллельна следу foα;. Эллипс может быть построен по его большой и малой осям или по отдельным точкам.

Рис.10. Пересечение цилиндра фронтально-проецирующей плоскостью

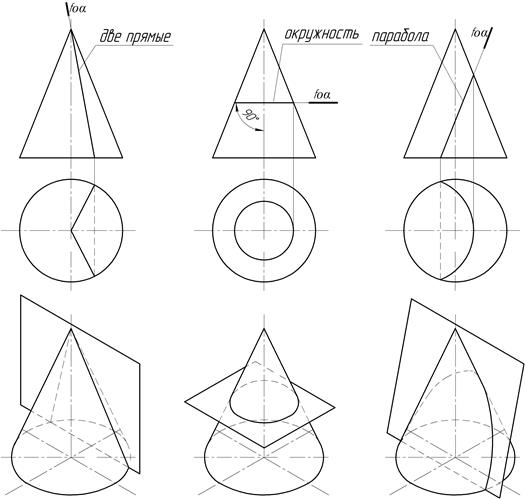
4.5. Сечение конуса проецирующей плоскостью – конические сечения

Ли­нией пересечения боковой поверхности прямого кругового конуса с плоскостью могут быть:

– две прямые - образующие конуса (рис.11а), если плоскость проходит через вершину конуса;

– окруж­ность (рис.11б), если плоскость перпендикулярна к оси конуса;

– парабола (рис.11в), если плоскость параллельна одной образую­щей конуса;

– гипербола (рис.11г ), если плоскость параллельна двум образующим конуса;

– эллипс (рис.11д, е),если плоскость пересекает все образующие конуса и не перпендикулярна к его оси.

а) б) в)

г) д) е)

Рис.11. Сечения конуса фронтально-проецирующей плоскостью

На рис. 12 построены проек­ции конуса, рассеченного фрон­тально проецирующей плоскостью α (задана своим фронтальным следом foα;),которая пересекает его поверхность по эллипсу. У эллипса большая ось – АВ=А"В";, малая ось CD расположена на середине большой оси и равна отрезку С' D'. Проекции С' и D' построены с по­мощью параллели поверхности (окружности), радиус которой опре­деляется точкой Т. Аналогично строятся все точки сечения.Точки 1 данного сечения принадлежат профильным очерковым образующим конуса. Они отделяют видимую в профильной проек­ции часть сечения (точки 1"' - C "' -A "'- D"'-1 "')от невидимой (точки 1"' -В"' -1"').

Рис.12. Пересечение конуса фронтально-проецирующей плоскостью

 

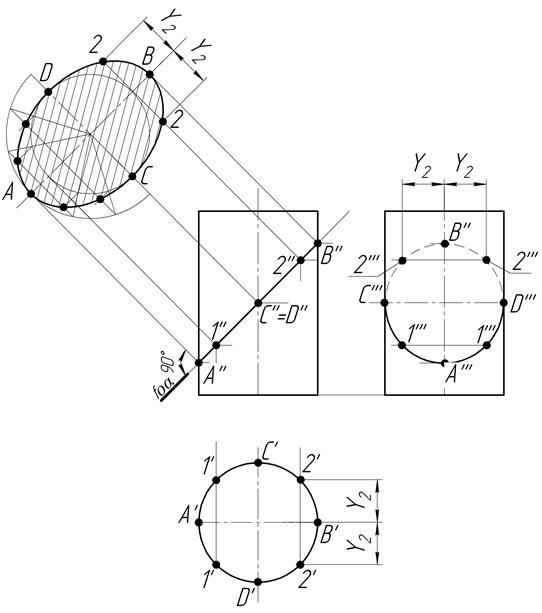
Горизонтальная проекция эллипса сечения не может быть ок­ружностью, профильная же проекция может ею быть. Эллипс A – B – C – D является натуральным видом сечения. Он может быть построен по осям или с помощью размера Y ряда точек.

При построении линии пересечения конуса с горизонтально про­ецирующей плоскостью α (задана своим горизонтальным следом hoα;), которая пересекает его по­верхность по гиперболе, используем параллели поверхности(рис. 13).

Рис.13. Пересечение конуса горизонтально-проецирующей плоскостью

 

В пе­ресечении их горизонтальных проекций (окружностей) с проекцией hoα плоскости намечаем горизонтальные проекции 1', …,7' точек линии сечения. На фронтальных проекциях этих параллелей строим фронтальные проекции 1",..., 7" соответствующих точек. Верхняя точка 4 сечения – вершина гиперболы – принадлежит параллели, которая касается проекции hoα. Проекции 3'" и 5" принадлежат очерковым образующим конуса. Фигура 1... 7 является натураль­ным видом сечения.