Классический метод расчета. 2. Составление характеристического уравнения цепи.1. Правила коммутации: iL (0-) = iL (0+) = 0 А, uC (0-) = uC (0+) = J . R2 = 20 B. 2. Составление характеристического уравнения цепи. 2.1.Совместное решение однородной системы дифференциальных уравнений. Составляем систему дифференциальных уравнений для мгновенных значений токов и напряжений по законам Кирхгофа:
Методом исключения получаем из данной системы дифференциальное неоднородное уравнение
Соответствующее ему характеристическое уравнение имеет вид
i11(1/(pC) + R1) - i22(1/(pC)) + i33 . 0 = E(p), -i11 (1/(pC) + i22 (R2 + pL + 1/(pC)) - i33R2 = 0, i11. 0 - i22R2 + i33R2 = UJ (p),
i11(1/pC + R1) - i22 (1/(pC)) + UJ . 0 = E/p, -i11(1/pC) + i22(R2 + pL + 1/pC) + 0 . UJ = J·R2, i11 . 0 - i22R2 + 1 . UJ = -J·R2.
i11св(1/(pC) + R1) - i22св (1/(pC)) + UJсв. 0 = 0, -i11св (1/(pC)) + i22св (R2 + pL + 1/pC) + 0 . UJсв = 0, i11св . 0 - i22свR2 + 1 . UJсв = 0. Данная система алгебраических уравнений имеет решение, отличное от нулевого только тогда, когда ее определитель равен нулю:
или
Таким образом, характеристическое уравнение в результате преобразования принимает вид
2.3. Метод входного сопротивления. Удалим источники из цепи в соответствии с известным правилом: источники ЭДС заменяются короткозамкнутыми участками, ветви с источниками тока размыкаются. В произвольной ветви разорвав цепь, запишем входное сопротивление:
Заменив jw на p, получим
Приравняв данное выражение нулю (z (р) = 0) и произведя необходимые преобразования, получим характеристическое уравнение цепи
Подставим значения параметров цепи: p2 + 700p + 300000 = 0. Корни характеристического уравнения p1 = - 350 + j421,308, p2 = - 350 - j421,308 являются комплексными сопряженными, следовательно, переходный процесс в цепи имеет колебательный характер. 3. Определение принужденной составляющей. Рассматриваемая цепь в принужденном режиме имеет вид (рис. 2.3)
i1пр = 1/3 (A).
Рис. 2.3 4. Определение свободной составляющей. Для цепей, характеристические числа которых имеют комплексные сопряженные значения, свободная составляющая определяется в виде i1св(t) = e- dt(A1 cos wt + A2 sin wt), где d - декремент затухания, w - частота свободных колебаний определяются через корни характеристического уравнения p1,2 = - d + jw. Таким образом, в выражении i1св необходимо определить постоянные интегрирования А1 и А2. Вычисление их ведется с помощью системы уравнений, составленных для момента t = 0+:
4.1. Определение значений
Дифференцируя выражение для i1 (t), получим
Произведя необходимые преобразования и подстановки в системе уравнений Кирхгофа, получим
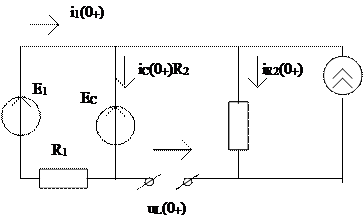
Подставив соответствующие значения uC и iL в момент t = 0+, рассчитаем i¢1 (0+) = - 250 A/с. 4.2. Определение i1(0+) и i¢1(0+) с использованием резистивных схем замещения в момент t = 0+. Схема замещения в 0+ для величин токов и напряжений изображена на рис. 2.4
ЕС = uС(0-) J = iL(0-)
Рис. 2.4 По II закону Кирхгофа получим
Для построения схемы замещения в (0+) для производных токов и напряжений необходимо определить начальные значения:
Таким образом, следует определить iC(0+) и uL(0+) с помощью уже полученной схемы замещения: а) для определения uL(0+) составим уравнение по II закону Кирхгофа: UL(0+) - iR2(0+) R2 = - UC(0+); подставив значения, получим UL(0+) = 0, следовательно, б) iC(0+) = i1(0+) = 0,5 A, следовательно, При построении схемы замещения в 0+ для производных следует: источники заменить на аналогичные источники с ЭДС или задающим током, равным соответственно производной от данных в задании, номиналы резисторов остаются неизменными, емкости и индуктивности же замещаются в соответствии со следующим правилом – емкости с нулевыми начальными условиями ( ветви с индуктивностями, имеющими нулевые начальные условия ( Таким образом, осуществляется операция дифференцирования, адекватная дифференцированию системы уравнений Кирхгофа. В нашем случае, когда в цепи действуют источники постоянных воздействий, источники ЭДС заменяются короткозамкнутыми участками (т.к. Таким образом, схема замещения в t = 0+ для производных имеет вид (рис. 2.5). Определим
4.3. Определение постоянных интегрирования:
421,308 A2 - 350 A1 = - 250. Решив данную систему уравнений, получим А1 = 0,1667, А2 = - 0.455. 5. Определение полного решения. Полное решение следует искать в виде i1(t) = i1пр + i1св. С учетом производных расчетов получим
Для удобства построения графика преобразуем полученное выражение в синусоидальную форму:
(+ p) прибавляется к аргументу, так как угол y имеет отрицательный знак
т.е. если рассматривать единичную окружность, данный угол находится во II четверти координатной плоскости. Угол yi определяется в радианах, так как свободная частота измеряется в рад/с. Таким образом, искомый ток i1(t) = 1/3 + e-350t 0.485 sin (421.308t + 2.788).
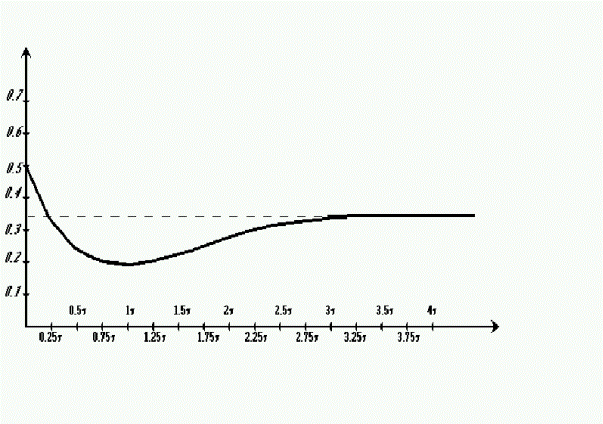
6. Построение графика изменения тока i (t). Оценим соотношение между постоянной времени экспоненты и периодом синусоиды. Постоянная времени экспоненты texp = 1/8 = 0,00286 с. Период синусоиды Tsin = 1/f = 2p/w = 0,0149 с. В связи с тем, что tехр << Tsin, график строится по точкам. Результаты расчетов значений тока i1(t) записаны в табл. 2.2., а график изменения i1 (t) изображен на рис. 2.6.
Таблица 2.2
|
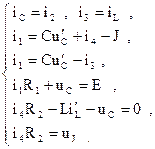
2.2. Алгебраизация дифференциальных уравнений. Для получения характеристических уравнений записывается система уравнений по методу контурных токов, которая в последствии переписывается в алгебраической форме с помощью вспомогательного символа p, заменяющего операцию дифференцирования, и 1/p, заменяющего операцию интегрирования:
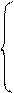Так как i33 = J, следовательно,
и, соответственно, для свободных составляющих токов:
,
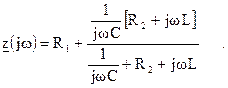
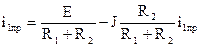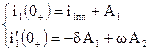
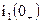и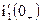 
с использованием системы уравнений Кирхгофа. В данном случае cоставляется система уравнений Кирхгофа. Методом исключения выражается значение тока i1(0+) через известные значения uC(0+) и i2(0+):
.
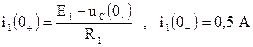
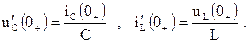
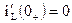= 5000 B/с.
) заменяются короткозамкнутыми участками, с ненулевыми начальными условиями(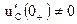
) – противодействующими источниками ЭДС с 
,
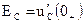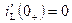) размыкаются, в случае ненулевых начальных условий (
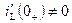) индуктивности заменяют на содействующие источники тока с 
.
), а ветви с источниками тока размыкаются (т.к.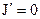 
).
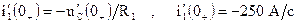
Рис. 2.5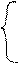
1/3 + А1 = 0,5,
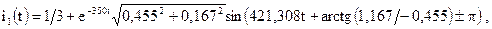
и положительный знак 
,
