Метод пространства состояний
При расчете цепи методом пространства состояний режим ее работы описывается матричными уравнениями:
причем, уравнение (1) - дифференциальное, а уравнение (2) - алгебраическое. В этих уравнениях: X = [ хi (t) ] - матрица-столбец переменных состояния, i изменяется в пределах [1; n ]; X¢ = [ хi (t) ] - матрица-столбец производных (скоростей изменения) переменных состояния; Y = [yj (t)] - матрица-столбец выходных реакций или вектор выхода, j изменяется в пределах [ 1; l]; V = [vк(t)]-матрица-столбец внешних воздействий или вектор входа, k изменяется в пределах [ 1; m ]; n - порядок электрической цепи; m - количество задающих источников; l - количество искомых выходных реакций; A, B, C, D - матрицы связей для исследуемой цепи. Матрицы связей A, B, C, D определяются с помощью уравнений Кирхгофа или с помощью канонической процедуры построения матриц связей. Каноническая процедура не требует предварительного составления уравнений Кирхгофа, так как элементы матриц A,B,C,D являются псевдопередаточными коэффициентами вспомогательных резистивных цепей. Покажем алгоритм получения матриц A, B, C, D на примере цепи II порядка, содержащей источник напряжения и источник тока, для которой уравнения состояния в развернутом виде запишутся:
В этой системе i1, i2 - искомые выходные токи (реакции). В общем случае это могут быть любые токи и напряжения в любых ветвях. Объединим полученные уравнения в матричное уравнение, содержащее расширенную матрицу реакций и переменных состояния:
Так как данное матричное уравнение является верным для любого момента времени t
Для определения искомых коэффициентов применим метод наложения (принцип суперпозиции). Если в уравнении (5) попеременно полагать все начальные значения iL (0+), uC (0+), Е1 (0+), J2 (0+) равными нулю, кроме одного, приравниваемого единице, то значения элементов расширенной матрицы i¢L (0+), u¢C (0+), i1 (0+), i2 (0+) совпадут с элементами соответствующего столбца матриц А, В, С, D. Принимая во внимание, что
можно свести задачу расчета коэффициентов матриц связей к рассмотрению четырех (в нашем конкретном случае, когда выходных реакций две) резистивных схем для момента t = 0+, в каждой из которых остается только один источник: i L (0+) = 1 или u C (0+) = 1 или Е 1 (0+) = 1 или J 2 (0+) = 1, а прочие источники исключают в соответствии с традиционными правилами - источники ЭДС заменяются короткозамкнутыми участками, ветви с источниками тока разрываются. Для наглядности результаты расчетов записывают в таблицу, подматрицы которой совпадают с матрицами А, В, С, D:
|

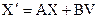 , (1)
, (1) , (2)
, (2)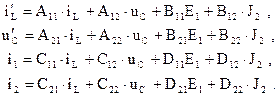 (3)
(3) (4)
(4)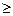 0+, т.е. значения коэффициентов матриц A, B, C, D являются величинами постоянными, то правомерной является следующая зависимость:
0+, т.е. значения коэффициентов матриц A, B, C, D являются величинами постоянными, то правомерной является следующая зависимость: (5)
(5)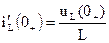 и
и 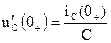 ,
,


