Расчет послекоммутационной цепи2. Определение корней характеристического уравнения 2.1. Составим характеристическое уравнение по методу входного сопротивления:
Рис. 1.4 а
2.2. Проверим правильность полученных результатов методом, основанным на определении постоянной времени цепи. Для индуктивной цепи первого порядка t = L / RЭ, где RЭ - эквивалентное сопротивление пассивной цепи, полученной из рассматриваемой путем удаления источников, относительно зажимов реактивного элемента (в нашем случае индуктивности). Правило удаления источников: ветви с источниками тока обрываются, источники напряжения замыкаются накоротко. В нашем случае пассивная цепь имеет вид (рис. 1.4 б):
t = L / RЭ = 0,2 / 542.857 = 0,368 мc. Следовательно, p = - 1 / t = - 1 / 0,368 = 2714,286 c-1. 3. Запишем полное решение в виде суммы принужденной и свободной составляющей:
4. Расчет принужденной составляющей. Цепь в принужденном режиме будет иметь вид (рис. 1.5):
Рис. 1.5
5. Расчет свободной составляющей. Схема замещения в 0+ представлена на рис. 1.6, где JL1 = iL(0-) = 0,345 A.
Рис. 1.6
Рис. 1.7 а
Рис. 1.7 б
Определим постоянную интегрирования: i4 (0+) = 0,211+ A1 = 0,1874; A1 = -0,0236. Таким образом, i4 (t) = 0,211- 0,0236 e-271t на промежутке t = (0+, tk2), где t = 0+ – момент первой коммутации.
|
;
.
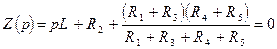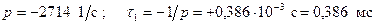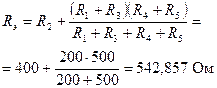
Рис. 1.4 б
.
;
.
;
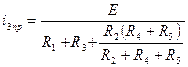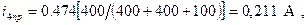
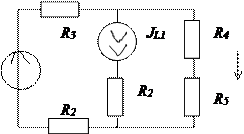
Определим ток i4(0+) методом наложения:
;
;
.
;
.
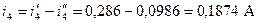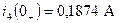