Проверка статистических гипотез о законе распределения СВ
1.2.2.1. Критерий согласия χ2 Пирсона В качестве оценок параметров нормального закона примем точечные оценки для математического ожидания и дисперсии:
Алгоритм проверки гипотезы: 1. Провести измерения X и получить выборку x n; 2. Построить вариационный ряд; 3. Исключить грубые ошибки; 4. Определить число интервалов 5. Определить границы интервалов; 6. Определить количество элементов попадающих в интервал; 7. Задать гипотезу о плотности распределения f0 (x); 8.Определить вероятность попадания случайной величины в полуинтервал (xj-1; xj), равную pj: где l j– длина интервала. 9.Рассчитать значение реализации статистики проверки гипотезы:
10.Задать уровень значимости α; 11.С помощью таблиц распределения 12.Принять или отклонить гипотезу по правилу: если если Расчет значения функции f 0(x) будем проводить по формуле:
Зададим вероятность, а =0,05 практически невозможного события, заключающегося в том, что сумма относительных отклонений оценки плотности распределения от значения функции плотности распределения, принятой в качестве гипотезы, не превзойдет значения Значение параметра После расчета реализации статистики проверки статистической гипотезы о нормальном распределении (наблюдаемого значения критерия), получили Результаты расчетов приведены в Приложении 5.
|

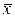 =295,8,
=295,8,  =29,428.
=29,428.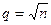 ;
;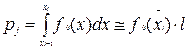 j,
j,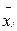 - середина l j,
- середина l j,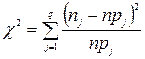 , где q –количество интервалов;
, где q –количество интервалов; Пирсона, по входам α и k = q - r -1 определить
Пирсона, по входам α и k = q - r -1 определить 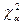 , здесь r – количество параметров предполагаемого закона распределения;
, здесь r – количество параметров предполагаемого закона распределения;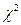 <
< 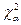 , гипотеза принимается
, гипотеза принимается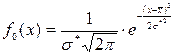 , используя при этом встроенную функцию MS Excel НОРМРАСП, параметры которой соответственно равны значению
, используя при этом встроенную функцию MS Excel НОРМРАСП, параметры которой соответственно равны значению 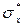 , четвертый параметр равен 0, что соответствует возвращению функцией значения плотности распределения нормального закона распределения.
, четвертый параметр равен 0, что соответствует возвращению функцией значения плотности распределения нормального закона распределения.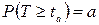 . Если выполняется условие:
. Если выполняется условие: 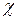 2 Пирсона, исходя из значений вероятности a и числа степеней свободы k = q-r -1, где r- количество параметров предполагаемого закона распределения.
2 Пирсона, исходя из значений вероятности a и числа степеней свободы k = q-r -1, где r- количество параметров предполагаемого закона распределения.


