Построение статистических оценок математического ожидания и дисперсии
Точечные оценки Рассчитаем реализацию точечной оценки математического ожидания (выборочное среднее):
Рассчитаем реализацию точечной оценки дисперсии (исправленную выборочную дисперсию):
Интервальные оценки
Доверительная вероятность, с которой доверительный интервал накроет истинное значение параметра закона распределения случайной величины:
Рассчитаем границы доверительного интервала для математического ожидания. Реализация точечной оценки математического ожидания Из таблиц распределения Стьюдента по значениям k =(n -1) и
Границы доверительного интервала для математического ожидания
Полученный доверительный интервал для математического ожидания:
Рассчитаем границы доверительного интервала для дисперсии. Рассчитаем значения:
Из таблицы k =(n – 1)=34 и
Границы доверительного интервала рассчитаем по формулам:
Полученный доверительный интервал для дисперсии:
|

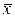 =
= 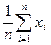 =295,8 сек.
=295,8 сек.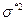 =
= 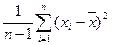 = 866,047 сек 2.
= 866,047 сек 2. =1 – α = 0,95.
=1 – α = 0,95.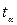 :
: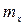 :
: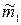 =
= 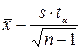 = 285,5433,
= 285,5433,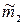 =
=  = 306,0567.
= 306,0567. = (285,5433; 306,0567).
= (285,5433; 306,0567).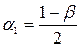 = 0,025,
= 0,025, 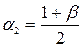 = 0,975.
= 0,975. - распределения, по входам k =(n – 1)=34 и
- распределения, по входам k =(n – 1)=34 и 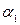 =0,025,
=0,025,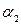 =0,975 найдем значения критических точек
=0,975 найдем значения критических точек 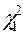 и
и 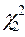 :
: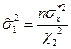 = 583,297,
= 583,297,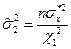 = 1530,41.
= 1530,41.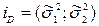 = (583,297; 1530,41).
= (583,297; 1530,41).


