Приложения. Приложение 1. Исключение грубых ошибок
Приложение 1. Исключение грубых ошибок
|
| A
| B
| C
| D
| E
| F
| | №
| Xi
| Xср
|
|
| Xi
| Xср
| |
|
| 2580,64
|
|
|
| 368,64
| |
|
| 2284,84
|
|
|
| 492,84
| |
|
| 1831,84
|
|
|
| 686,44
| |
|
| 1664,64
|
|
|
| 852,64
| |
|
| 1505,44
|
|
|
| 1102,24
| |
|
| 1211,04
|
|
|
| 1169,64
| |
|
| 1075,84
|
|
|
| 1239,04
| |
|
| 888,04
|
|
|
| 1383,84
| |
|
| 718,24
|
|
|
| 1866,24
| |
|
| 519,84
|
|
|
| 2043,04
| |
|
| 316,84
|
|
|
| 2420,64
| |
|
| 249,64
|
|
|
|
| |
|
| 116,64
|
|
|
|
| |
|
| 60,84
|
|
|
|
| |
|
| 33,64
|
|
|
|
| |
|
| 23,04
|
|
|
|
| |
|
| 3,24
|
|
|
|
| |
|
| 0,64
|
|
|
|
| |
|
| 10,24
|
|
|
|
| |
|
| 17,64
|
|
|
|
| |
|
| 84,64
|
|
|
|
| |
|
| 125,44
|
|
|
|
| |
|
| 201,64
|
|
|
|
| |
|
| 295,84
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
| Xср=
| 295,8
|
| ta(при а=0,05) =
| 2,84
|
| |
| S=
| 29,4286775
|
|
|
|
| |
|
| Xmin=
|
|
|
|
| |
|
| Xmax=
|
|
|
|
| |
|
| Xmin>Xср-Sta
|
|
|
|
| |
|
| 245>212,1637 Xmin не является грубой ошибкой
| |
|
| Xmax<Xср+Sta
|
|
|
|
| |
|
| 345<379,4363 Xmax не является грубой ошибкой
| |
|
|
|
|
|
|
| | | | | | | | | |
Приложение 2. Интервальная таблица
| Номер интервала
|
|
|
|
|
|
| | Границы интервалов
|
245;
261,666
|
261,666;
278,333
|
278,333;
|
295;
311,666
|
311,666;
328,333
|
328,333;
| Длина интервала 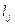
| 16,666
| 16,666
| 16,666
| 16,666
| 16,666
| 16,666
| Частота интервала 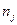
|
|
|
|
|
|
| Относительная частота интервалов 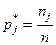
|
0,143
| 0,143
| 0,171
| 0,200
| 0,143
| 0,200
| Плотность относительной частоты 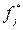 = = 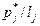
| 0,009
| 0,009
| 0,010
| 0,012
| 0,009
| 0,012
| Середина интервала 
| 253,33
| 270,00
| 286,67
| 303,33
| 320,00
| 336,67
| | F**(x)
| 0,143
| 0.286
| 0.457
| 0.657
| 0.800
|
|
Приложение 3. Точечные и интервальные оценки математического ожидания и дисперсии
|
| A
| B
| C
| D
| E
| F
| G
|
| |
| №
| Xi
|
| (Xi-Xcp)^2
|
|
|
|
| |
|
|
|
| 2580,64
|
|
|
|
| |
|
|
|
| 2284,84
|
|
|
|
| |
|
|
|
| 1831,84
|
|
|
|
| |
|
|
|
| 1664,64
|
|
|
|
| |
|
|
|
| 1505,44
|
|
|
|
| |
|
|
|
| 1211,04
|
|
|
|
| |
|
|
|
| 1075,84
|
|
|
|
| |
|
|
|
| 888,04
|
|
|
|
| |
|
|
|
| 718,24
|
|
|
|
| |
|
|
|
| 519,84
|
|
|
|
| |
|
|
|
| 316,84
|
|
|
|
| |
|
|
|
| 249,64
|
|
|
|
| |
|
|
|
| 116,64
|
|
|
|
| |
|
|
|
| 60,84
|
|
|
|
| |
|
|
|
| 33,64
|
|
|
|
| |
|
|
|
| 23,04
|
|
|
|
| |
|
|
|
| 3,24
|
|
|
|
| |
|
|
|
| 0,64
|
|
|
|
| |
|
|
|
| 10,24
|
|
|
|
| |
|
|
|
| 17,64
|
|
|
|
| |
|
|
|
| 84,64
|
|
|
|
| |
|
|
|
| 125,44
|
|
|
|
| |
|
|
|
| 201,64
|
|
|
|
| |
|
|
|
| 295,84
|
| B
| 0,95
|
| |
|
|
|
| 368,64
|
|
|
|
| |
|
|
|
| 492,84
|
| tb=
| 2,0322445
|
| |
|
|
|
| 686,44
|
| m1=
| 285,5433
|
| |
|
|
|
| 852,64
|
| m2
| 306,0567
|
| |
|
|
|
| 1102,24
|
| a1
| 0,025
|
| |
|
|
|
| 1169,64
|
| a2
| 0,975
|
| |
|
|
|
| 1239,04
|
| t1
| 51,96602
|
| |
|
|
|
| 1383,84
|
| t2
| 19,80624
|
| |
|
|
|
| 1866,24
|
| б1^2
| 583,297
|
| |
|
|
|
| 2043,04
|
| б2^2
| 1530,41
|
| |
|
|
|
| 2420,64
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
| mx=
| 295,8
| б^2=
| 866,047059
|
|
| |
|
|
|
|
| S=
| 29,42868
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
Приложение 4. Критерий Колмогорова
|
| X
| Y
| Fo(x)
| F*(x)
| |F*(x)-Fo(x)|
|
|
|
| |
|
| -1,72621
| 0,042155056
| 0,028571
| 0,013583628
|
| Xcp=
| 295,8
| |
|
| -1,62427
| 0,052159526
| 0,057143
| 0,004983331
|
| S*=
| 29,42868
| |
|
| -1,45436
| 0,072922751
| 0,085714
| 0,012791535
|
|
|
| |
|
| -1,3864
| 0,082811975
| 0,114286
| 0,031473739
|
|
|
| |
|
| -1,31844
| 0,093677889
| 0,142857
| 0,049179253
|
|
|
| |
|
| -1,18252
| 0,118499715
| 0,171429
| 0,052928856
|
|
|
| |
|
| -1,11456
| 0,132519705
| 0,200000
| 0,067480295
|
|
|
| |
|
| -1,01262
| 0,155621399
| 0,228571
| 0,07295003
|
|
|
| |
|
| -0,91068
| 0,18123297
| 0,257143
| 0,075909887
|
|
|
| |
|
| -0,77475
| 0,219242373
| 0,285714
| 0,066471913
|
|
|
| |
|
| -0,60485
| 0,272638607
| 0,314286
| 0,041647108
|
|
|
| |
|
| -0,53689
| 0,295671361
| 0,342857
| 0,047185782
|
|
|
| |
|
| -0,36699
| 0,356813623
| 0,371429
| 0,014614948
|
|
|
| |
|
| -0,26505
| 0,395486401
| 0,400000
| 0,004513599
|
|
|
| |
|
| -0,19709
| 0,421879858
| 0,428571
| 0,006691571
|
|
|
| |
|
| -0,16311
| 0,435217406
| 0,457143
| 0,021925451
|
|
|
| |
|
| -0,06116
| 0,47561397
| 0,485714
| 0,010100316
|
|
|
| |
|
| -0,02718
| 0,489156342
| 0,514286
| 0,025129372
|
|
|
| |
|
| 0,108737
| 0,54329464
| 0,542857
| 0,000437497
|
|
|
| |
|
| 0,142718
| 0,556743523
| 0,571429
| 0,014685048
|
|
|
| |
|
| 0,31262
| 0,622715398
| 0,600000
| 0,022715398
|
|
|
| |
|
| 0,380581
| 0,648242966
| 0,628571
| 0,019671537
|
|
|
| |
|
| 0,482523
| 0,685282602
| 0,657143
| 0,028139745
|
|
|
| |
|
| 0,584464
| 0,720545881
| 0,685714
| 0,034831596
|
|
|
| |
|
| 0,652425
| 0,742936426
| 0,714286
| 0,028650711
|
|
|
| |
|
| 0,754366
| 0,774685323
| 0,742857
| 0,03182818
|
|
|
| |
|
| 0,890288
| 0,813344383
| 0,771429
| 0,041915811
|
|
|
| |
|
| 0,992229
| 0,839457191
| 0,800000
| 0,039457191
|
|
|
| |
|
| 1,128151
| 0,870371981
| 0,828571
| 0,041800552
|
|
|
| |
|
| 1,162132
| 0,877409021
| 0,857143
| 0,020266163
|
|
|
| |
|
| 1,196112
| 0,88417361
| 0,885714
| 0,001540676
|
|
|
| |
|
| 1,264073
| 0,896898107
| 0,914286
| 0,017387607
|
|
|
| |
|
| 1,467956
| 0,928941895
| 0,942857
| 0,013915247
|
|
|
| |
|
| 1,535917
| 0,937720606
| 0,971429
| 0,033707966
|
|
|
| |
|
| 1,671839
| 0,952721927
| 1,000000
| 0,047278073
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| max=
| 0,075909887
| |
|
|
|
|
|
|
| tнабл=
| 0,075909887
| |
|
|
|
|
|
|
| tкр=
| 0,22425
| |
| tнабл<tкр,гипотеза принимается
|
|
|
|
| | | | | | | | | | | | Приложение 5. Критерий Пирсона
| A
| B
| C
| D
| E
| F
| G
| H
| |
| Xi
| Xi+1
| Xср
| nj
| Xсрnj
| (Xср-x)
| (Xср-x)^2*nj
| |
|
| 261,6667
| 253,3333
|
| 1266,667
| -50
|
| |
| 261,6667
| 278,3333
|
|
|
| -33,3333
| 5555,556
| |
| 278,3333
|
| 286,6667
|
|
| -16,6667
| 1666,667
| |
|
| 311,6667
| 303,3333
|
| 2123,333
|
|
| |
| 311,6667
| 328,3333
|
|
|
| 16,66667
| 1388,889
| |
| 328,3333
|
| 336,6667
|
| 2356,667
| 33,33333
| 7777,778
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
| x =
| 295,8
| s =
| 29,42868
| |
|
|
|
|
|
|
|
| |
| l
| f
| pj
| npj
| (nj-npj)^2/npj
| ∑(nj-nf)^2/npj
|
| |
| 16,66667
| 0,004786
| 0,079765
| 2,791762
| 1,74668
| 7,481774
|
| |
| 16,66667
| 0,009231
| 0,153847
| 5,384653
| 0,027478
|
|
| |
| 16,66667
| 0,012919
| 0,215314
| 7,535993
| 0,313067
|
|
| |
| 16,66667
| 0,013119
| 0,218655
| 7,652912
| 0,055703
|
|
| |
| 16,66667
| 0,009667
| 0,16112
| 5,639186
| 0,07245
|
|
| |
| 16,66667
| 0,005169
| 0,086147
| 3,015154
| 5,266395
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
| t=
| 7,481774
|
| ta =
| 7,81473
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
| t<ta,гипотеза принимается
|
|
|
|
Приложение 6. Таблица значений функции j(x)= 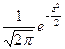
|
|
|
|
|
|
|
|
|
|
|
| | 0,0
| 0,3989
|
|
|
|
|
|
|
|
|
| | 0,1
|
|
|
|
|
|
|
|
|
|
| | 0,2
|
|
|
|
|
|
|
|
|
|
| | 0,3
|
|
|
|
|
|
|
|
|
|
| | 0,4
|
|
|
|
|
|
|
|
|
|
| | 0,5
|
|
|
|
|
|
|
|
|
|
| | 0,6
|
|
|
|
|
|
|
|
|
|
| | 0,7
|
|
|
|
|
|
|
|
|
|
| | 0,8
|
|
|
|
|
|
|
|
|
|
| | 0,9
|
|
|
|
|
|
|
|
|
|
| | 1,0
| 0,2420
|
|
|
|
|
|
|
|
|
| | 1,1
|
|
|
|
|
|
|
|
|
|
| | 1,2
|
|
| 18Э5
|
|
|
|
|
|
|
| | 1,3
|
|
|
|
|
|
|
|
|
|
| | 1,4
|
|
|
|
|
|
|
|
|
|
| | 1,5
|
|
|
|
|
|
|
|
|
|
| | 1,6
|
|
|
|
|
|
|
|
|
|
| | 1,7
|
|
|
|
|
|
|
|
|
|
| | 1,8
|
|
|
|
|
|
|
|
|
|
| | 1,9
|
|
|
|
|
|
|
|
|
|
| Таблица значений функции j(x)= 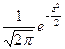
|
|
|
|
|
|
|
|
|
|
|
| | 2,0
| 0,0540
|
|
|
|
|
|
|
|
|
| | 2,1
|
|
|
|
|
|
|
|
|
|
| | 2,2
|
|
|
|
|
|
|
|
|
|
| | 2,3
|
|
|
|
|
|
|
|
|
|
| | 2,4
|
|
|
|
|
|
|
|
|
|
| | 2,5
|
|
|
|
|
|
|
|
|
|
| | 2,6
|
|
|
|
|
|
|
|
|
|
| | 2,7
|
|
|
|
|
|
|
|
|
|
| | 2,8
|
|
|
|
|
|
|
|
|
|
| | 2,9
|
|
|
|
|
|
|
|
|
|
| | 3,0
| 0,0044
|
|
|
|
|
|
|
|
|
| | 3,1
|
|
|
|
|
|
|
|
|
|
| | 3,2
|
|
|
|
|
|
|
|
|
|
| | 3,3
|
|
|
|
|
|
|
|
|
|
| | 3,4
|
|
|
|
|
|
|
|
|
|
| | 3,5
|
|
|
|
|
|
|
|
|
|
| | 3,6
|
|
|
|
|
|
|
|
|
|
| | 3,7
|
|
|
|
|
|
|
|
|
|
| | 3,8
|
|
|
|
|
|
|
|
|
|
| | 3,9
|
|
|
|
|
|
|
|
|
|
|
Приложение 7. Таблица значений функции F(x)= 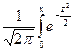 dz dz
| X
| Ф (X)
| X
| Ф (х)
| X
| Ф (X)
| X
| Ф (х)
| | 0,00
| 0,0000
| 0,32
| 0,1255
| 0,64
| 0,2389
| 0,96
| 0,3315
| | 0,01
| 0,0040
| 0,33
| 0,1293
| 0,65
| 0,2422
| 0,97
| 0,3340
| | 0,02
| 0,0080
| 0,34
| 0,1331
| 0,66
| 0,2454
| 0,98
| 0,3365
| | 0,03
| 0,0120
| 0,35
| 0,1368
| 0,67
| 0,2486
| 0,99
| 0,3389
| | 0,04
| 0,0160
| 0,36
| 0,1406
| 0,68
| 0,2517
| 1,00
| 0,3413
| | 0,05
| 0,0199
| 0,37
| 0,1443
| 0,69
| 0,2549
| 1,01
| 0,3438
| | 0,06
| 0,0239
| 0,38
| 0,1480
| 0,70
| 0,2580
| 1,02
| 0,3461
| | 0,07
| 0,0279
| 0,39
| 0,1517
| 0,71
| 0,2611
| 1,03
| 0,3485
| | 0,08
| 0,0319
| 0,40
| 0,1554
| 0,72
| 0,2642
| 1,04
| 0,3508
| | 0,09
| 0,0359
| 0,41
| 0,1591
| 0,73
| 0,2673
| 1,05
| 0,3531
| | 0,10
| 0,0398
| 0,42
| 0,1628
| 0,74
| 0,2703
| 1,06
| 0,3554
| | 0,11
| 0,0438
| 0,43
| 0,1664
| 0,75
| 0,2734
| 1,07
| 0,3577
| | 0,12
| 0,0478
| 0,44
| 0,1700
| 0,76
| 0,2764
| 1,08
| 0,3599
| | 0,13
| 0,0517
| 0,45
| 0,1736
| 0,77
| 0,2794
| 1,09
| 0,3621
| | 0,14
| 0,0557
| 0,46
| 0,1772
| 0,78
| 0,2823
| 1,10
| 0,3643
| | 0,15
| 0,0596
| 0,47
| 0,1808
| 0,79
| 0,2852
| 1,11
| 0,3665
| | 0,16
| 0,0636
| 0,48
| 0,1844
| 0,80
| 0,2881
| 1,12
| 0,3686
| | 0,17
| 0,0675
| 0,49
| 0,1879
| 0,81
| 0,2910
| 1,13
| 0,3708
| | 0,18
| 0,0714
| 0,50
| 0,1915
| 0,82
| 0,2939
| 1,14
| 0,3729
| | 0,19
| 0,0753
| 0,51
| 0,1950
| 0,83
| 0,2967
| 1,15
| 0,3749
| | 0,20
| 0,0793
| 0,52
| 0,1985
| 0,84
| 0,2995
| 1,16
| 0,3770
| | 0,21
| 0,0832
| 0,53
| 0,2019
| 0,85
| 0,3023
| 1,17
| 0,3790
| | 0,22
| 0,0871
| 0,54
| 0,2054
| 0,86
| 0,3051
| 1,18
| 0,3810
| | 0,23
| 0,0910
| 0,55
| 0,2088
| 0,87
| 0,3078
| 1,19
| 0,3830
| | 0,24
| 0,0948
| 0,56
| 0,2123
| 0,88
| 0,3106
| 1,20
| 0,3849
| | 0,25
| 0,0987
| 0,57
| 0,2157
| 0,89
| 0,3133
| 1,21
| 0,3869
| | 0,26
| 0,1026
| 0,58
| 0,2190
| 0,90
| 0,3159
| 1,22
| 0,3883
| | 0,27
| 0,1064
| 0,59
| 0,2224
| 0,91
| 0,3186
| 1,23
| 0,3907
| | 0,28
| 0,1103
| 0,60
| 0,2257
| 0,92
| 0,3212
| 1,24
| 0,3925
| | 0,29
| 0,1141
| 0,61
| 0,2291
| 0,93
| 0,3238
| 1,25
| 0,3944
| | 0,30
| 0,1179
| 0,62
| 0,2324
| 0,94
| 0,3264
|
|
| | 0,31
| 0,1217
| 0,63
| 0,2357
| 0,95
| 0,3289
|
|
|
Таблица значений функции F(x)= 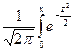 dz dz
| X
| Ф (X)
| X
| Ф (х)
| X
| Ф (X)
| X
| Ф (х)
| | 1,26
| 0,3962
| 1,59
| 0,4441
| 1,92
| 0,4726
| 2,50
| 0,4938
| | 1,27
| 0,3980
| 1,60
| 0,4452
| 1,93
| 0,4732
| 2,52
| 0,4941
| | 1,28
| 0,3997
| 1,61
| 0,4463
| 1,94
| 0,4738
| 2,54
| 0,4945
| | 1,29
| 0,4015
| 1,62
| 0,4474
| 1,95
| 0,4744
| 2,56
| 0,4948
| | 1,30
| 0,4032
| 1,63
| 0,4484
| 1,96
| 0,4750
| 2,58
| 0,4951
| | 1,31
| 0,4049
| 1,64
| 0,4495
| 1,97
| 0,4756
| 2,60
| 0,4953
| | 1,32
| 0,4066
| 1,65
| 0,4505
| 1,98
| 0,4761
| 2,62
| 0,4956
| | 1,33
| 0,4082
| 1,66
| 0,4515
| 1,99
| 0,4767
| 2,64
| 0,4959
| | 1,34
| 0,4099
| 1,67
| 0,4525
| 2,00
| 0,4772
| 2,66
| 0,4961
| | 1,35
| 0,4115
| 1,68
| 0,4535
| 2,02
| 0,4783
| 2,68
| 0,4963
| | 1,36
| 0,4131
| 1,69
| 0,4545
| 2,04
| 0,4793
| 2,70
| 0,4965
| | 1,37
| 0,4147
| 1,70
| 0,4554
| 2,06
| 0,4803
| 2,72
| 0,4967
| | 1,38
| 0,4162
| 1,71
| 0,4564
| 2,08
| 0,4812
| 2,74
| 0,4969
| | 1,39
| 0,4177
| 1,72
| 0,4573
| 2,10
| 0,4821
| 2,76
| 0,4971
| | 1,40
| 0,4192
| 1,73
| 0,4582
| 2,12
| 0,4830
| 2,78
| 0,4973
| | 1,41
| 0,4207
| 1,74
| 0,4591
| 2,14
| 0,4838
| 2,80
| 0,4974
| | 1,42
| 0,4222
| 1,75
| 0,4599
| 2,16
| 0,4846
| 2,82
| 0,4976
| | 1,43
| 0,4236
| 1,76
| 0,4608
| 2,18
| 0,4854
| 2,84
| 0,4977
| | 1,44
| 0,4251
| 1,77
| 0,4616
| 2,20
| 0,4861
| 2,86
| 0,4979
| | 1,45
| 0,4265
| 1,78
| 0,4625
| 2,22
| 0,4868
| 2,88
| 0,4980
| | 1,46
| 0,4279
| 1,79
| 0,4633
| 2,24
| 0,4875
| 2,90
| 0,4981
| | 1,47
| 0,4292
| 1,80
| 0,4641
| 2,26
| 0,4881
| 2,92
| 0,4982
| | 1,48
| 0,4306
| 1,81
| 0,4649
| 2,28
| 0,4887
| 2,94
| 0,4984
| | 1,49
| 0,4319
| 1,82
| 0,4656
| 2,30
| 0,4893
| 2,96
| 0,4985
| | 1,50
| 0,4332
| 1,83
| 0,4664
| 2,32
| 0,4898
| 2,98
| 0,4986
| | 1,51
| 0,4345
| 1,84
| 0,4671
| 2,34
| 0,4904
| 3,00
| 0,49865
| | 1,52
| 0,4357
| 1,85
| 0,4678
| 2,36
| 0,4909
| 3,20
| 0,49931
| | 1,53
| 0,4370
| 1,86
| 0,4686
| 2,38
| 0,4913
| 3,40
| 0,49966
| | 1,54
| 0,4382
| 1,87
| 0,4693
| 2,40
| 0,4918
| 3,60
| 0,499841
| | 1,55
| 0,4394
| 1,88
| 0,4699
| 2,42
| 0,4922
| 3,80
| 0,499928
| | 1,56
| 0,4406
| 1,89
| 0,4706
| 2,44
| 0,4927
| 4,00
| 0,499968
| | 1,57
| 0,4418
| 1,90
| 0,4713
| 2,46
| 0,4931
| 4,50
| 0,499997
| | 1,58
| 0,4429
| 1,91
| 0,4719
| 2,48
| 0,4934
| 5,00
| 0,499997
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Искусство подбора персонала. Как оценить человека за час Искусство подбора персонала. Как оценить человека за час...
Этапы творческого процесса в изобразительной деятельности По мнению многих авторов, возникновение творческого начала в детской художественной практике носит такой же поэтапный характер, как и процесс творчества у мастеров искусства...
Тема 5. Анализ количественного и качественного состава персонала Персонал является одним из важнейших факторов в организации. Его состояние и эффективное использование прямо влияет на конечные результаты хозяйственной деятельности организации.
|
Словарная работа в детском саду Словарная работа в детском саду — это планомерное расширение активного словаря детей за счет незнакомых или трудных слов, которое идет одновременно с ознакомлением с окружающей действительностью, воспитанием правильного отношения к окружающему...
Правила наложения мягкой бинтовой повязки 1. Во время наложения повязки больному (раненому) следует придать удобное положение: он должен удобно сидеть или лежать...
ТЕХНИКА ПОСЕВА, МЕТОДЫ ВЫДЕЛЕНИЯ ЧИСТЫХ КУЛЬТУР И КУЛЬТУРАЛЬНЫЕ СВОЙСТВА МИКРООРГАНИЗМОВ. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА БАКТЕРИЙ Цель занятия. Освоить технику посева микроорганизмов на плотные и жидкие питательные среды и методы выделения чистых бактериальных культур. Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения...
|
|

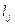
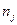
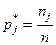
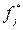 =
= 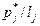

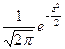
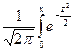 dz
dz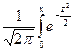 dz
dz


