Критерий согласия Колмогорова
Критерий Колмогорова позволяет проверить гипотезу о виде функции распределения случайной величины и ее параметрах. Выдвинем следующую гипотезу: случайная величина распределена по нормальному закону с параметрами:
В качестве значений параметров берем рассчитанные ранее значения реализаций точечных оценок этих параметров. Рассчитаем значение реализации статистики проверки гипотезы t:
где x i –элемент выборки, Расчет значения функции F0(x) можно осуществлять по формуле:
Алгоритм проверки гипотезы: 1. Провести измерения Х и получить выборку х n; 2. Построить вариационный ряд; 3. Исключить грубые ошибки; 4. Построить статистическую функцию распределения; 5. Задать гипотезу, что F 0(x) есть функция распределения Х; 6. Подсчитать t, при этом для вычисления значений функции распределения F 0(x) требуется нормализовать выборку значений случайной величины Х, т.е. перейти к случайной величине Y, которая является нормированной случайной величиной Х: y i=(xi- 7. Задать а и с помощью таблицы Колмогорова найти t α; 8. Принять или отклонить гипотезу; Зададим вероятность а =0,05 практически невозможного события, заключающегося в том, что оценка функции распределения отклонится от значения функции принятой в качестве гипотезы, на величину большую, чем t α P( Если выполняется условие: t < t α, то гипотеза принимается. Значение параметра t α возьмем из таблицы Колмогорова, исходя из значений вероятности а и объема выборки n: t α=0,22425. После выполнения алгоритма проверки гипотезы получили t =0,075909, которое не превышает значение параметра t α. Следовательно, гипотеза о нормальном распределении случайной выборки принимается. Результаты расчетов приведены в Приложении 4.
Выводы
В результате выполненных расчетов было установлено следующее: 1. При проведении опыта не было выявлено грубых ошибок измерения. 2. Точечные оценки математического ожидания и дисперсии соответственно равны:
3. В результате проведенной проверки соответствия закона распределения случайной величины – времени, за которое выполняется загрузка файла на интернет хостинг – нормальному закону, было установлено, что с вероятностью
Список литературы 1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 6-е, стер. – М.: Высш. шк., 2001. 2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов.-8-е изд., стер.- М.: Машиностроение, 2002. 3. Ивченко Г.И., Медведев Ю.И. Математическая статистика: Учеб. пособие для втузов.- М.: Высш. шк., 1984. 4. Кожевников Ю.В. Теория вероятностей и математическая статистика: Учебное пособие для вузов. М.: Машиностроение, 2002. 5. Ю. В. Кожевников «Введение в математическую статистику» КГТУ им. А. Н. Туполева, 1996. 6. Роднищев Н.Е. Курс теории вероятностей и математической статистики: Учебное пособие. Казань: Изд-во Казан. гос. техн. ун-та, 2001. 7. Большев Л.Н., Смирнов Н.В. «Таблицы математической статистики». М: Наука,1983.
|

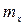 =295,8 и
=295,8 и 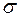 *=29,42868.
*=29,42868.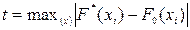 ,
,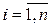 .
.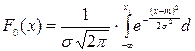 x, используя при этом встроенную функцию MS Excel НОРМРАСП, параметры которой соответственно равны значению xi, точечной оценке математического ожидания
x, используя при этом встроенную функцию MS Excel НОРМРАСП, параметры которой соответственно равны значению xi, точечной оценке математического ожидания 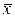 , точечной оценке среднеквадратического отклонения
, точечной оценке среднеквадратического отклонения 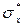 , значение четвертого параметра равно 1, что соответствует возвращению встроенной функцией значения функции распределения нормального закона.
, значение четвертого параметра равно 1, что соответствует возвращению встроенной функцией значения функции распределения нормального закона. .
.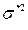 =886,047059;
=886,047059; = 0,95 практически достоверного события выборочные данные согласуются с гипотезой о нормальном законе распределения исследуемой случайной величины.
= 0,95 практически достоверного события выборочные данные согласуются с гипотезой о нормальном законе распределения исследуемой случайной величины.


