УДК 621.1.016.001
ББК 31:3
Ó Д. Степанов, Н. Степанова, 2014 ЗМІСТ
ПЕРЕДМОВА.. 5 1 ЗАГАЛЬНІ ПОНЯТТЯ ТА ВИЗНАЧЕННЯ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ 6 1.1 Історичний розвиток моделювання. 6 1.2 Класифікація методів наукового пізнання. 7 1.3 Рівні наукового пізнання. 8 1.4 Основні поняття та визначення моделювання. 9 1.5 Різновиди моделювання. 10 2 СИСТЕМИ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ (СЛАР) 12 2.1 Основні визначення. 12 2.2 Класифікація методів розв’язання СЛАР. 13 2.3 Точні методи розв’язання СЛАР. 14 2.4 Наближені методи розв’язання СЛАР. 15 3 НЕЛІНІЙНІ РІВНЯННЯ.. 21 3.1 Постановка задачі 21 3.2 Класифікація нелінійних рівнянь. 22 3.3 Визначення кількості дійсних коренів алгебраїчного рівняння. 23 3.4 Методи відокремлення коренів алгебраїчного рівняння. 23 3.5 Методи розв’язання нелінійних рівнянь. 24 3.6 Методи розв’язання систем нелінійних рівнянь. 27 3.7 Розв’язання систем нелінійних рівнянь з використанням 4 ДИФЕРЕНЦІЙНІ РІВНЯННЯ.. 33 4.1 Постановка задачі 33 4.2 Метод Ейлера розв’язання диференційних рівнянь. 33 4.3 Метод Рунге-Кутта розв’язання диференційних рівнянь. 34 4.4 Метод прогнозу та корекції розв’язання диференційних 5 НАБЛИЖЕННЯ ФУНКЦІЙ, АПРОКСИМАЦІЯ, ІНТЕРПОЛЯЦІЯ. МЕТОД НАЙМЕНШИХ КВАДРАТІВ.. 38 5.1 Постановка задачі 38 5.2 Поліноміальная інтерполяція. 39 5.3 Метод найменших квадратів. 40 6 КЛАСИФІКАЦІЯ МАТЕМАТИЧНИХ МОДЕЛЕЙ.. 44 6.1 Постановка задачі 44 6.2 Класифікація моделей в залежності від параметрів моделі 44 6.3 Класифікація моделей за змістовною побудовою.. 45 6.4 Класифікація моделей в залежності від мети моделювання. 46 6.5 Класифікація математичних моделей залежно від методів реалізації 47 7 ЕТАПИ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ.. 49 7.1 Етапи побудови моделі 49 7.2 Обстеження об’єкту моделювання. 49 7.3 Математична постановка задачі 51 7.4 Якісний аналіз моделі, перевірка коректності 52 7.5 Обґрунтування і вибір методу розв’язання задачі 52 7.6 Реалізація моделі у вигляді програми. 52 7.7 Перевірка адекватності моделі 53 7.8 Практичне використання розробленої моделі 54 8 МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ В РАМКАХ ДИПЛОМНОГО ПРОЕКТУВАННЯ.. 55 8.1 Системний підхід до досліджень. 55 8.2 Методика побудови математичних моделей. 56 8.3 Розробка математичного опису теплогідродинамічних 8.4 Загальна характеристика математичної моделі 8.5 Представлення отриманих результатів числових 9 ОПТИМІЗАЦІЯ В ТЕПЛОЕНЕРГЕТИЧНИХ ЗАДАЧАХ.. 65 9.1 Критерії оптимізації теплоенергетичних об’єктів. 65 9.2 Методи пошуку екстремуму. 65 10 КЛАСИФІКАЦІЯ ТА ДЖЕРЕЛА ПОХИБОК. ПОХИБКИ РОЗРАХУНКОВИХ ВЕЛИЧИН.. 69 10.1 Класифікація похибок за джерелами виникнення. 69 10.2 Похибки наближених чисел. 69 10.3 Похибки розрахункових величин. 71 10.4 Поняття про імовірну оцінку похибки. 72 10.5 Обчислення без точного врахування похибок. 73 11 ЗАВДАННЯ НА КОНТРОЛЬНУ РОБОТУ ДЛЯ СТУДЕНТІВ ЛІТЕРАТУРА.. 78 ГЛОСАРІЙ.. 79
ПЕРЕДМОВА
Даний навчальний посібник призначений для студентів денної та заочної форм навчання напряму підготовки 6.050601 – Теплоенергетика. Посібник підготовлений відповідно до навчальної програми дисципліни “Математичні методи і моделі”. Публікації технічної україномовної навчальної літератури з питань моделювання теплогідродинамічних процесів у елементах обладнання не приділяється достатньої уваги. Тому, на думку авторів, даний посібник буде корисним як для підготовки студентів-теплоенергетиків, так і для інших суміжних спеціальностей. Викладений матеріал дозволить готуватись до лекційних занять, лабораторних робіт, поточного та підсумкового контролю знань, виконувати розділи курсового та дипломного проектування. Значна кількість прикладів із розв’язанням та завдань дозволить якісно організувати самостійну роботу студентів. Значна увага приділена рекомендація по підготовці розділу з математичного моделювання в рамках підготовки бакалаврської дипломної роботи. Авторами розглянуті методи розв’язання систем лінійних та нелінійних рівнянь, диференційних рівнянь, методи інтерполяції та апроксимації даних, елементи теорії похибок. В тексті посібника наведені завдання на контрольну роботу студентам заочної форми навчання за напрямом підготовки 6.050601 – Теплоенергетика. Автори вдячні рецензентам за корисні поради і зауваження в процесі рецензування і підготовки рукопису.
Автори
1 ЗАГАЛЬНІ ПОНЯТТЯ ТА ВИЗНАЧЕННЯ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ
1.1 Історичний розвиток моделювання
У століття Інтернету і космічних технологій важко уявити інженера-розробника без комп'ютера. Сучасні дослідження настільки наукоємні, що просто фізично неможливо обійтися без допомоги обчислювальної машини. Колосальні обсяги інформації вимагається аналізувати під час дослідження процесів в різних областях науки і техніки. В теплоенергетиці досліджуються всілякі процеси горіння палива в різних моделях топок, процеси течії парорідинних сумішей в проточних частинах турбогенераторів (розрахунок нагріву металу і його розширення при різних граничних умовах, ґрунтується на рішенні рівнянь теплопровідності) і розплавлених металів, що є теплоносієм першого контуру в парогенераторах атомних електричних станцій, досліджується вплив струменів пари на поверхню лопаток турбіни, що необхідно для запобігання їх корозійного зносу, так само досліджуються процеси протікання ядерних реакцій в тепловидільних елементах (ТВЕЛах) тощо. Насправді більшість процесів в теплоенергетиці вже давно вивчено. Дослідження проходять по оптимізації цих процесів і вивченню глибинної суті явищ для досягнення максимального ефекту при розробці енергетичного устаткування. Тут і потрібна математична модель. Взагалі елементи математичного моделювання використовувалися з самого початку появи точних наук, і не випадково, що деякі методи обчислень носять імена таких корифеїв науки, як Ньютон і Ейлер, а слово «алгоритм» походить від імені середньовічного арабського вченого Аль-Хорезмі. Друге «народження» цієї методології припало на кінець 40-х-начало 50-х років XX століття і було обумовлене принаймні двома причинами. Перша з них – поява ЕОМ (комп’ютерів), хоча і скромних за нинішніми мірками, які позбавили вчених величезної за об’ємом рутинної обчислювальної роботи. Друга – безпрецедентне соціальне замовлення – виконання національних програм СРСР і США по створенню ракетно-ядерного щита, які не могли бути реалізовані традиційними методами. Математичне моделювання справилося з цією задачею: ядерні вибухи і польоти ракет і супутників були заздалегідь «здійснені» в надрах ЕОМ за допомогою математичних моделей і лише потім втілені на практиці. Цей успіх багато в чому визначив подальші досягнення методології, без застосування якої в розвинутих країнах жоден великомасштабний технологічний, екологічний або економічний проект тепер всерйоз не розглядається (сказане справедливо і по відношенню до деяких соціально-політичних проектів). Зараз математичне моделювання вступає в третій принципово важливий етап свого розвитку, «вбудовуючись» в структури так званого інформаційного суспільства. Вражаючий прогрес засобів переробки, передачі і зберігання інформації відповідає світовим тенденціям до ускладнення і взаємного проникнення різних сфер людської діяльності. Без володіння інформаційними «ресурсами» не можна і думати про рішення все більш укрупнюються і все більш різноманітних проблем, що стоять перед світовою спільнотою. Проте інформація як така часто мало що дає для аналізу і прогнозу, для прийняття рішень і контролю за їх виконанням. Потрібні надійні способи переробки інформаційної «сировини» в готовий «продукт», тобто в точне знання. Історія методології математичного моделювання переконує: вона може і повинна бути інтелектуальним ядром інформаційних технологій, всього процесу інформатизації суспільства. Технічні, екологічні, економічні і інші системи, що вивчаються сучасною наукою, більше не піддаються дослідженню (в потрібній повноті і точності) звичайними теоретичними методами. Прямий натурний експеримент над ними довгий, дорогий, часто або небезпечний, або просто неможливий, оскільки багато хто з цих систем існує в «єдиному екземплярі». Ціна помилок і прорахунків в роботі з ними неприпустимо висока. Тому математичне (ширше – інформаційне) моделювання є неминучою складовою науково-технічного прогресу.
1.2 Класифікація методів наукового пізнання
Методи наукового пізнання прийнято підрозділяти по ступеню їх спільності, тобто,по широті застосовності в процесі наукового дослідження (рис. 1.1) на загальні, загальнонаукові і частковонаукові. Із загальних методів в історії пізнання відомі два: діалектичний і метафізичний. Це загально-філософські методи. При метафізичному підході об'єкти і явища навколишнього світу розглядаються ізольовано один від одного, без урахування їх взаємних зв'язків і як би в застиглому, фіксованому, незмінному стані. Діалектичний підхід, навпаки, припускає вивчення об'єктів, явищ зі всім багатством їх взаємозв'язків, з урахуванням реальних процесів їх зміни, розвитку. З середини XIX в., в період третьої наукової революції метафізичний метод почав все більше і більше витіснятися з природознавства діалектичним методом. Загальнонаукові методи використовуються в самих різних областях науки, тобто мають вельми широкий міждисциплінарний спектр застосування. Класифікація цих методів тісно зв'язана з поняттям рівнів наукового пізнання.
1.3 Рівні наукового пізнання
Розрізняють два рівні наукового пізнання: емпіричний і теоретичний. Одні загальнонаукові методи застосовуються тільки на емпіричному рівні (спостереження, експеримент, вимірювання), інші - тільки на теоретичному (ідеалізація, формалізація), але є і такі (наприклад, моделювання), які використовуються як на теоретичному так і на емпіричному рівні. Емпіричний рівень наукового пізнання характеризується безпосереднім дослідженням реально існуючих, чуттєво сприйманих об'єктів. На цьому рівні шляхом проведення спостережень, виконання різноманітних вимірювань, постановки експериментів здійснюється процес накопичення інформації про досліджувані об'єкти, явища, проводиться первинна систематизація одержуваних фактичних даних у вигляді таблиць, схем, графіків і т.п. Крім того, на емпіричному рівні наукового пізнання – як наслідок узагальнення наукових фактів – можливо формулювання деяких емпіричних закономірностей. Теоретичний рівень наукового пізнання властивий раціональній (логічній) ступені пізнання. На даному рівні відбувається розкриття найглибших, істотних сторін, зв’язків, закономірностей, що відносяться до об'єктів, що вивчаються, явище. Теоретичний рівень - більш високий ступінь в науковому пізнанні. Результатами теоретичного пізнання стають гіпотези, теорії, закони. Виділяючи в науковому дослідженні два різні рівні – емпіричний і теоретичний, не слід, проте, відривати їх один від одного і протиставляти, оскільки вони тісно взаємопов’язані. Емпіричний рівень виступає як основа, фундамент теоретичного осмислення наукових фактів і одержуваних статистичних даних. В той же час теоретичне мислення спирається на наочні образи (у тому числі схеми, графіки і т.п.), з якими має справу емпіричний рівень дослідження. У свою чергу емпіричний рівень наукового пізнання не може існувати без досягнень теоретичного рівня. Емпіричне дослідження звичайно спирається на певну теоретичну конструкцію, яка визначає напрям цього дослідження, обумовлює і обґрунтовує вживані при цьому методи. До групи частково-наукові методів наукового пізнання відносяться методи, що використовуються тільки в рамках досліджень якої-небудь конкретної науки або якого-небудь конкретного явища. Кожна приватна наука (біологія, хімія, геологія і т.д.) має свої специфічні методи дослідження. Як правило, частково-наукові методи містять в різних поєднаннях ті або інші загальнонаукові методи пізнання, базуються на них і можуть включати спостереження, вимірювання, індуктивні або дедуктивні висновки і т.д. Характер поєднання різних методів і його використовування залежить від умов дослідження, природи об'єктів, що вивчаються. Таким чином, частково-наукові методи не відірвані від загальнонаукових, навпаки, тісно пов'язані з ними, а також із загальним діалектичним методом, який як би переламується через них. Наприклад, загальний діалектичний принцип розвитку виявився в біології у вигляді відкритого Ч.Дарвіном природно-історичного закону еволюції тварин і рослинних видів. До сказаного залишається додати, що будь-який метод сам по собі ще не зумовлює успіху в пізнанні тих або інших сторін матеріальної дійсності. Важливо ще уміти правильно використовувати його в процесі пізнання. Отже, моделювання – метод пізнання навколишнього світу, який можна віднести до загальнонаукових методів, вживаних як на емпіричному, так і на теоретичному рівні пізнання.
1.4 Основні поняття та визначення моделювання
Моделювання - метод пізнання навколишнього світу, який можна віднести до загальнонаукових методів, вживаних як на емпіричному, так і на теоретичному рівні пізнання. Об’єкт моделювання – будь-який реальний процес, явище або ефект, існуючий поза нашої свідомості і є предметом теоретичного вивчення або практичної діяльності. Таким чином під об'єктом або оригіналом розуміється окремий елемент або сукупність елементів предметної області, поведінка яких досліджується з метою встановлення основних закономірностей або особливостей їх функціонування. Предметна область моделювання - частина або фрагмент реальної дійсності, що містить цікавий для нас об'єкт, поведінка якого повинна бути досліджена. Цим визначенням закріплюється, що моделювання якого-небудь реально існуючого об'єкту не може виконуватися окремо, без встановлення його зв'язків з іншими об'єктами даної предметної області. Ця вимога має важливе методологічне значення для будь-якого виду моделювання, у тому числі математичного. Модель - штучно створений матеріальний або теоретичний образ реального об'єкта, що відображує його найбільш важливі і принципові властивості і дозволяє передбачати його поведінку на основі експерименту з моделлю. Матеріальна модель відтворює в більш простому або зменшеному вигляді структуру і основні риси, взаємозв'язки та відносини між елементами досліджуваного об'єкту. Частіше всього термін «модель» використовують для позначення: – модель як пристрій, що відтворює будову чи дію якого-небудь пристрою (зменшене, збільшене або в натуральну величину); – модель як аналог (креслення, графіка, плану, схеми, опису и т.д.) якого-небудь явища, процесу або предмета. – модель як зразок майбутнього виробу. До процесу моделювання висувають такі вимоги: - дослідження на моделі повинно бути економічніше, простіше, безпечніше ніж на оригіналі; - повинно бути відомо правило розрахунку характеристик оригінала на основі даних, отриманих на моделі.
1.5 Різновиди моделювання
Прийнято розрізняти три види моделювання: фізичне; аналогове; математичне. Фізичне моделювання дозволяє поглибити знання про явища, їх кількісно оцінити полегшити математичний опис об’єкту. Результати є більш наочними. Недоліком фізичного моделювання є необхідність створювати нову модель для нового процесу. Важче із моделями ланцюга процесів. Приходиться ув’язувати моделі процесів, створювати систему управління моделями, а це буває складніше, ніж створити систему управління реальним об’єктом. Під час фізичного моделювання в теплоенергетиці використовується теорія подібності [1]. Подібні явища описуються однаковими рівняннями: рух ньютонівських рідин – рівнянням Нав’є-Стокса і нерозривності, теплові процеси – рівняннями Фур’є-Кірхгофа, Нав’є-Стокса та нерозривності тощо. При моделюванні необхідно задати умови однозначності. Тобто для подібних процесів геометрична форма, наприклад, повинна бути однакова, а розміри пропорційні. При фізичному моделюванні неможливо витримати подібність за всіма критеріями подібності. Якщо однакові критерії Фруда (v2/(g×l)), то не можуть бути однакові критерії Рейнольдса Re=(w×l/n). Аналогове моделювання (analogus - схожий) побудоване на тому, що різні процеси можуть описуватись однаковими рівняннями, або аналогічними якісно рівняннями. Аналогічними рівняннями називають такі, в яких величини відрізняються, але всі оператори однакові і розставлені в однаковому порядку. Величини в аналогічних рівняннях називають аналогами. Метод вивчення процесів за допомогою аналогів називають аналоговим моделюванням. Наприклад, рух потоку в каналі, розповсюдження теплової енергії та електричний струм – різні процеси, але вони описуються аналогічними рівняннями. Основні величини, що характеризують ці процеси – різні, але між ними є аналогія: – гідравлічний напір – температура – напруга; – термічний опір – гідравлічний опір – електричний опір; – теплоємність – поперечний переріз посудини – ємність конденсатора. Може скластися враження, що процес моделюється «без математики», але математична аналогія вже наперед доведена. Математичне моделювання – це теоретично-експериментальний метод пізнавальної діяльності, це метод визначення і пояснення явищ, процесів і систем (об’єктів-оригіналів) на основі створення нових об’єктів - математичних моделей. Інше визначення – "Дослідження технологічного або іншого процесу із використанням сукупності математичних співвідношень (рівностей, нерівностей, логічних умов тощо), що описують процес". Математична модель – це формальна система, що є кінцевою сукупністю символів і досить суворих правил, визначених цими символами для певного об’єкта із деякими власними відношеннями, символами або константами. Або "Сукупність математичних виразів, що визначають кінцеві характеристики (параметри стану, показники ефективності) процесу в залежності від початкового стану, зміни зовнішніх умов та часу". Нарешті, найлаконічніше визначення математичної моделі: «Рівняння, яке виражає ідею». Математична модель, як правило, враховує лише ті властивості (атрибути) об’єкта-оригінала, які відображають, визначають і є цікавими з точки зору цілей і задач конкретного дослідження. Будь-який об’єкт є невичерпним в своїх властивостях і співвідношеннях, тому не можна вивчати одразу все нескінченне багатство змісту об’єкту. Відповідно, в залежності від цілей моделювання, при розгляді одного і того ж об’єкта-оригінала з різних точок зору і в різних аспектах останній може мати різні математичні описи і, як наслідок, бути представленим різними математичними моделями. Контрольні запитання 1. Дайте характеристику історичного розвитку моделювання. 2. Наведіть класифікацію методів пізнання. 3. Поясніть відмінність метафізичного та діалектичного методів пізнання. Наведіть приклади. 4. Поясніть відмінність емпіричного та теоретичного рівнів пізнання. Наведіть приклади. 5. Поясніть взаємозв’язок методів пізнання. Наведіть приклади поєднання різних методів пізнання. 6. Дайте визначення поняття "моделювання". 7. Поясніть відмінність предмета об’єкта моделювання. Наведіть приклади. 8. Поясніть поняття "модель". Наведіть різні тлумачення цього терміну. 9. Дайте характеристику фізичного моделювання. 10. Дайте характеристику аналогового моделювання. 11. Дайте характеристику математичного моделювання.
2 СИСТЕМИ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ (СЛАР)
2.1 Основні визначення
Система n лінійних рівнянь з невідомими має наступний вигляд:
При цьому через Величини Система називається однорідною, якщо всі вільні члени рівні нулю. Якщо хоча б один з вільних членів не рівний нулю, то система називається неоднорідною. Система називається квадратною, якщо кількість рівнянь рівне кількості невідомих. Рішенням системи називається така сукупність Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо у неї не існує жодного розв’язку. Сумісна система може мати більше одного розв’язку. Сумісна система називається визначеною, якщо вона має єдиний розв’язок. Сумісна система називається невизначеною, якщо у неї існує по крайній мірі два різних розв’язки. Лінійну систему зручно записувати в матричній формі
2.2 Класифікація методів розв’язання СЛАР Методи розв’язання СЛАР поділяють на точні та наближені (ітераційні) (рис. 2.1).
2.3 Точні методи розв’язання СЛАР
Метод Гауса (метод послідовного виключення елементів) Ідея методу полягає в наступному. Дана система лінійних рівнянь з n невідомими. Застосовуючи лінійні перетворення рівнянь, систему приводимо до еквівалентної трикутної системи наступного вигляду
В цій системі спочатку з останнього рівняння визначається величина, а потім послідовною підстановкою визначаються величини решти невідомих. Для виключення х1 до кожного рівняння, крім першого, додаємо перше рівняння домножене на (-аj1/a11), де j – номер рядка. Аналогічно виключаємо другу невідому. Домножаємо друге рівняння на (-аj2/a22).
|



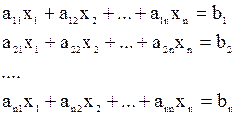 .
. позначені невідомі, які належить визначити.
позначені невідомі, які належить визначити. , що називають коефіцієнтами системи і величини
, що називають коефіцієнтами системи і величини  , що називають вільними членами, є відомими.
, що називають вільними членами, є відомими.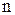 чисел
чисел  , яка при підстановці в систему на місце невідомих
, яка при підстановці в систему на місце невідомих  ,
, ,
,  ,
,  .
.
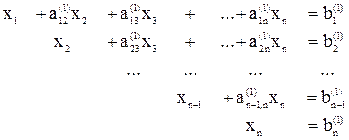 .
.


