Розв’язання. Представимо систему рівнянь у вигляді матриці А × Х = B
Представимо систему рівнянь у вигляді матриці А × Х = B
Лівий верхній коефіцієнт системи обираємо розв’язувальним елементом, тому перший рядок ділимо на 1, весь стовпчик під розв’язувальним елементом обнулюємо, і розраховуємо решту коефіцієнтів за правилом прямокутника
звідки
процедуру із другим та третім рядком
Отримаємо
Приклад 2.3. Розв’язати систему лінійних алгебраїчних рівнянь методом простих ітерацій та методом Зейделя з сумарною похибкою до 3%.
Для розв’язку приведемо систему до нормованого вигляду, отримаємо
Перевіримо таку систему на збіжність. Бачимо, що сума модулів коефіцієнтів при х1, х2 і х3 в рядках та стовпцях не перевищує 1, отже процес буде збіжним. Розв’яжемо систему методом простих ітерацій. Для нульового наближення приймемо х1(0) = 1,33, х2(0) = 3, х3(0) = – 0,111. Тоді перша ітерація х1(1)=1,33 – 0,333 × 3 – 0,25 × (-0,111) = 0,361, Друга ітерація дає х1(2)=1,33 – 0,333 × 2,63 – 0,25 × 1,85 = -0,00463, аналогічно х2(2) = 3,604, х3(2) = 1,43. Сумарна зміна результатів в порівнянні з попередньою ітерацією значна, тому виконуємо наступну ітерацію. Третя ітерація дає х1(3)= -0,225, х2(3) = 3,54, х3(2) = 1,89. Сумарна розбіжність з попередньою ітерацією значна. На восьмій ітерації х1(8)= -0,416, х2(8) = 3,82, х3(8) = 1,91. Розбіжність результатів в порівнянні з попередньою ітерацією складає 1,93%. Ту ж систему рівнянь розв’яжемо методом Зейделя. Перша ітерація х1(1) = 0,361 – аналогічно попередньому розв’язку, а х2(1) = 3 – 0,25 × 0,361 + 0,375 × (-0,111) = 2,87, х3(1) = -0,111 + 0,222 × 0,361 + + 0,556 × 2,87 = 1,56. Друга ітерація х1(2)= -0,0133, х2(2) = 3,59, х3(2) = 1,88. Після п’ятої ітерації х1(5)= -0,421, х2(8) = 3,83, х3(8) = 1,92. Розбіжність результатів в порівнянні з попередньою ітерацією складає 2,92%. Задачі для самостійної роботи
Приклад 2.4. Розв’язати систему лінійних алгебраїчних рівнянь методом Гауса, Гауса-Жордана, методом простих ітерацій, методом Зейделя
3 НЕЛІНІЙНІ РІВНЯННЯ
3.1 Постановка задачі
Нехай задане рівняння з однією змінною
Знайти точні значення коренів даного рівняння можна лише для найпростіших функцій: алгебраїчних многочленів не вище четвертого степеня, деяких многочленів степеня Універсальних методів для знаходження точних значень коренів алгебраїчних рівнянь степеня Нехай Нехай, Знаходження наближених коренів рівняння (3.1) складається з двох етапів: 1) відокремлення коренів, тобто знаходження досить малих відрізків, на кожному з яких міститься тільки один корінь рівняння; 2) обчислення коренів з наперед заданою точністю. Зазначимо, що корені рівняння (3.1) можуть бути дійсними і комплексними. Далі розглянемо обчислення лише дійсних коренів рівняння (3.1).
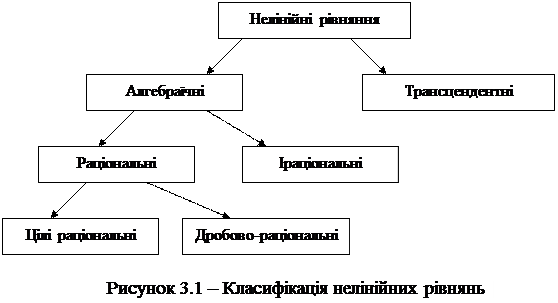
3.2 Класифікація нелінійних рівнянь
Класифікація нелінійних рівнянь наведена на рис. 3.1. Розглянемо означення та приклади різних типів нелінійних рівнянь.
Алгебраїчна функція є раціональною відносно змінної х, якщо над нею не виконується ніяких інших дій, крім додавання, віднімання, множення, ділення і піднесення до цілого степеня. Наприклад: Якщо у раціональну функцію змінна х не входить як дільник або не входить у вираз, який є дільником – функція є цілою раціональною. Вона визначена на всій числовій осі. Так, функції виду Якщо в раціональній функції хоча б один раз зустрічається ділення на змінну х або змінна х входить у вираз, який є дільником, то така функція є дробово-раціональною. Так, наприклад, функція Функція є іраціональною, якщо для отримання значення функції за даним значенням х необхідно виконати, крім чотирьох арифметичних дій (всіх або деяких), ще й обчислення кореня, при цьому х знаходиться під знаком радикалу. Другий великий клас функцій – трансцендентні функції. До них відносяться всі неалгебраїчні функції: показникові
3.3 Визначення кількості дійсних коренів алгебраїчного рівняння
Кількість дійсних додатних коренів алгебраїчного рівняння можна визначити приблизно за таким правилом: якщо рівняння повне, то кількість його додатних коренів дорівнює числу змін знака в послідовності коефіцієнтів або на парне число менша, а кількість від’ємних коренів - кількості сталості знака або на парне число менша.
3.4 Методи відокремлення коренів алгебраїчного рівняння
Для знаходження області існування коренів та визначення кількості коренів нелінійного рівняння використовують методи та теореми вищої математики.
|

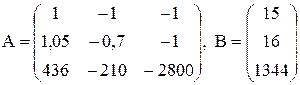 .
.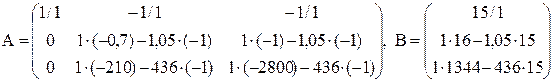
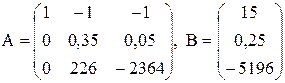 , виконаємо аналогічну
, виконаємо аналогічну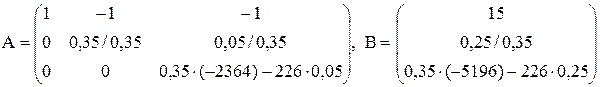
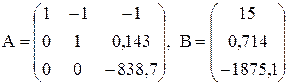 . З третього рівняння х3 = 2,236, після підстановки отриманих результатів в друге та перше рівняння отримаємо х2 = 0,395, х1 = 17,63.
. З третього рівняння х3 = 2,236, після підстановки отриманих результатів в друге та перше рівняння отримаємо х2 = 0,395, х1 = 17,63.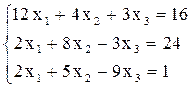 .
. .
.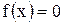 . (3.1)
. (3.1) і деяких трансцендентних функцій.
і деяких трансцендентних функцій.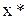 – точний корінь, а
– точний корінь, а 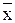 – його наближене значення. Кажуть, що корінь
– його наближене значення. Кажуть, що корінь 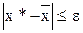 .
. і
і 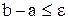 тоді а і b - наближені значення кореня
тоді а і b - наближені значення кореня  .
.
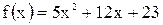 , або
, або 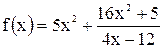 .
.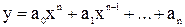 (де n – натуральне число або нуль,
(де n – натуральне число або нуль, 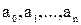 – будь-які дійсні числа, причому
– будь-які дійсні числа, причому  ) є цілими раціональними.
) є цілими раціональними.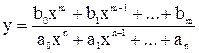 , (де m – натуральне число або нуль; n – натуральне число;
, (де m – натуральне число або нуль; n – натуральне число;  – будь-яке дійсне число
– будь-яке дійсне число 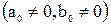 – є дробово-раціональною функцією, що визначена на всій числовій осі, за винятком тих точок, в яких знаменник перетворюється на нуль.
– є дробово-раціональною функцією, що визначена на всій числовій осі, за винятком тих точок, в яких знаменник перетворюється на нуль.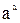 ; логарифмічна
; логарифмічна  , тригонометричні sin x, cos x, tg x, ctg x, зворотні тригонометричні arctg x, arcsin x, тощо.
, тригонометричні sin x, cos x, tg x, ctg x, зворотні тригонометричні arctg x, arcsin x, тощо.


