Метод простих ітерацій
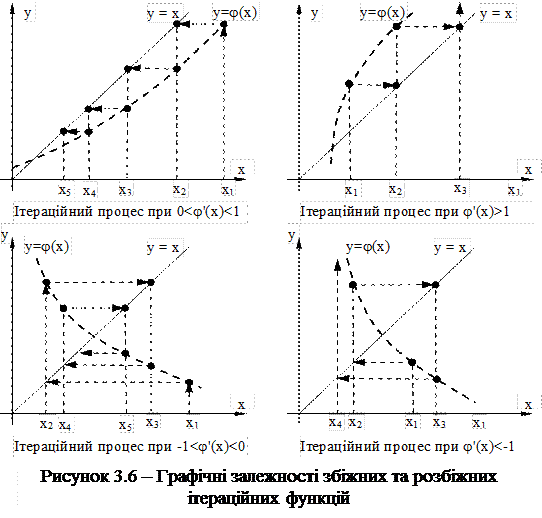
Для використання такого методу необхідно функцію перетворити до ітераційного вигляду х = j(х). Кожна наступна ітерація розраховується за формулою Не кожне рівняння можна розв’язати методом простих ітерацій, тому що ітераційний процес може бути збіжним або розбіжним. Збіжність ітераційного процесу залежить від величини похідної ітераційної функції (див. рис. 3.6). Умовою збіжності ітерацій є
Ітераційні методи стійкі до помилки, допущеної на одній з ітерацій, але за умови використання комп’ютерного розрахунку похибка, якщо вона є, повторюватиметься на всіх ітераціях. При цьому погіршуватиметься якість розв’язання. Зараз широко використовуються комбіновані методи, в яких поєднано швидкі ітераційні методи із надійними методами бісекції і хорд.
3.6 Методи розв’язання систем нелінійних рівнянь
Систему нелінійних рівнянь (СНР) можна представити у вигляді
На відміну від систем лінійних рівнянь для СНР не існує точних методів розв’язання. Лише дуже обмежену кількість систем можна вирішити безпосередньо. Наприклад, систему з двох рівнянь можна розв’язати графоаналітичним методом або можна одну невідому виразити через іншу і потім розв’язати відносно одної невідомої. Але абсолютну більшість систем вирішують ітераційними методами.
|
. Ітераційний процес припиняється за умов зменшення відстані між результатами послідовних ітерації менше за задану похибку.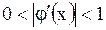
.
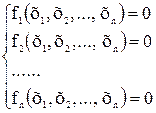. (3.2)
