Приклад 4. Побудова математичної моделі кожухотрубного теплообміннику.
Розробити математичну модель кожухотрубного теплообміннику, в якому нагрівається отцтово-водна суміш концентрацією 30% до температури Т=100 Тепловий баланс кожухотрубного теплообмінника описується системою рівнянь:
Перше рівняння описує баланс теплоти теплоносія, а друге – для нагріваючого продукту (рідини чи газу). Після ділення кожного з рівнянь системи на dt матимемо:
Вважаємо, що втрати теплоти Сталі параметри: маса продукту в теплообміннику mр, маса стінок mс, поверхня Sp, теплота фазового переходу r. Змінні параметри: температура стінки Тс, витрати теплоносія FТ, температура продукту на вході Тр та на виході Т/p теплообмінника, витрати Fр. Структурно-логічна схема кожухотрубного теплообмінника подана на рис.
Рис. Структурно-логічна схема об’єкту керування.
Змінні параметри об’єкту керування запишемо у вигляді:
Рівняння статики:
Запишемо ці рівняння у відносній формі, позначивши:
В результаті отримаємо:
Розділимо вираз на Введемо позначення:
Тоді ці рівняння матимуть вигляд:
Оскільки температура стінки Тс є проміжним параметром, вона вилучається з відповідного рівняння, для чого система рівнянь розв’язується відносно З останнього виразу знаходимо
Введемо нові позначення:
Тоді рівняння математичної моделі кожухотрубного теплообмінника матиме вигляд:
Це рівняння відповідає структурно-логічній схемі рисунка. Передаточна функція об’єкту керування з урахуванням часу запізнення за каналом регулювання матиме вигляд:
де Q1, Q2 – концентрації води та оцту в суміші; с1, с2 – їх теплоємності. Теплоємність оцту обчислюється за формулою:
де Т – температура, Оскільки теплоємність води дорівнює 4,19
а на його виході
Коефіцієнт тепловіддачі від стінок трубок до рідини, враховуючи, що пара при теплообміні конденсується, дорівнює 10,51 Обчислимо сталі часу:
З рівнянь статики знайдемо витрати пари, яка необхідна для нагрівання суміші, враховуючи, що r=39610,4 кДж/кг.
Коефіцієнти передачі:
Знайдемо параметри математичної моделі:
Підставивши знайдені значення величини, матимемо:
Отримана математична модель свідчить, що зв’язки між вихідними параметрами Тоді математична модель матиме вигляд:
Передаточна функція об’єкта керування за каналом регулювання буде:
Знайдемо час запізнення теплообмінника за каналом зміни навантаження та за каналом зміни регулюючого органу. Якщо змінюються тільки витрати рідини, а всі інші параметри незмінні, то:
де Якщо змінюється температура розчину, то:
За каналом зміни носія:
В відповідності з величиною часу запізнення передаточна функція об’єкту керування набуде вигляду
|

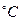 . Витрати цієї суміші становлять Fр=250 м3/год. Температура на вході Тр0=25
. Витрати цієї суміші становлять Fр=250 м3/год. Температура на вході Тр0=25 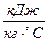 .
.
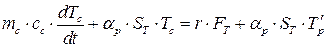 ;
; .
. незначні та ними можна знехтувати. Крім того, за допустимих відхилень температури зміна теплоємностей сс, ср, с’р незначна та нею можна також знехтувати. Вважаємо, що коефіцієнт тепловіддачі змінюється незначно.
незначні та ними можна знехтувати. Крім того, за допустимих відхилень температури зміна теплоємностей сс, ср, с’р незначна та нею можна також знехтувати. Вважаємо, що коефіцієнт тепловіддачі змінюється незначно.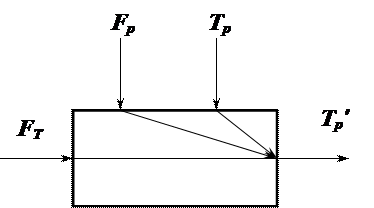

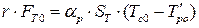 ,
,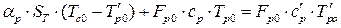 . Підставляючи значення змінних параметрів у відповідні співвідношення, після множення та нехтування складовими малого ступеня важливості, віднімання рівнянь статики матимемо:
. Підставляючи значення змінних параметрів у відповідні співвідношення, після множення та нехтування складовими малого ступеня важливості, віднімання рівнянь статики матимемо: ;
;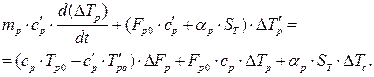
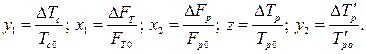
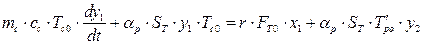 ;
; 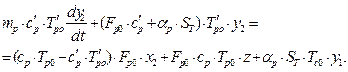
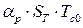 , а другий – на
, а другий – на 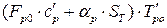 .
.
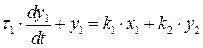 ;
; .
.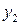 .
.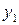 та
та 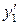 .
.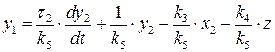 ;
; 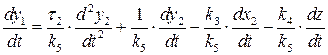 . Підставимо ці співвідношення у відповідне рівняння, після перетворень матимемо:
. Підставимо ці співвідношення у відповідне рівняння, після перетворень матимемо: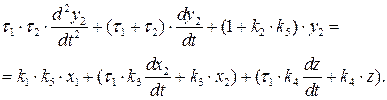
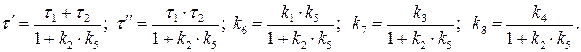
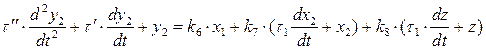 .
.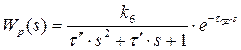 ; за каналом збурення:
; за каналом збурення: . Теплоємність суміші:
. Теплоємність суміші: ,
,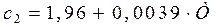 ,
,
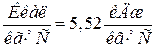 .
.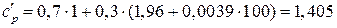
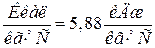 .
.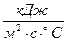 .
.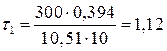 c;
c;  c.
c. кг/год.
кг/год.

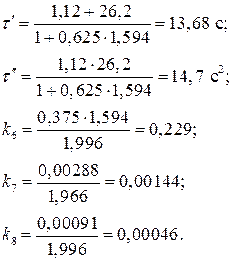
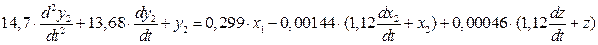 .
.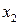 , z незначні, в практичних розрахунках ними можна знехтувати.
, z незначні, в практичних розрахунках ними можна знехтувати. .
.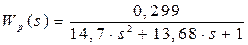 .
. ;
; .
.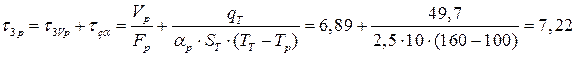 c.
c.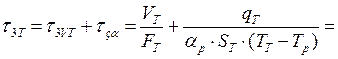
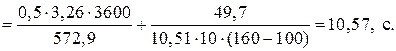
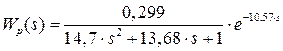 .
.


