Випарна установка в загальному випадку має 4 вихідні параметри. Для її дослідження необхідно скласти рівняння теплового і матеріального балансів.
Рівняння матеріалього балансу установки за концентрацію упареного розчину має вигляд:
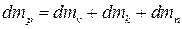 ; (6.48)
; (6.48)
де 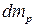 – маса цільового продукту, що надходить до установки;
– маса цільового продукту, що надходить до установки;  – маса цільового продукту, що накопичується в об’ємі V кубової частини;
– маса цільового продукту, що накопичується в об’ємі V кубової частини; 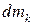 – маса продукту, що виходить з установки;
– маса продукту, що виходить з установки; 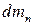 – маса продукту, що може витрачатися з вторинною парою.
– маса продукту, що може витрачатися з вторинною парою.
Ці величини визначаються за формулами:
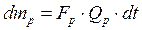 , (6.49)
, (6.49)
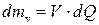 ,
, 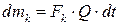
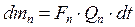 , (6.50)
, (6.50)
Тоді рівня 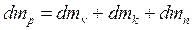 набуває вигляду:
набуває вигляду:
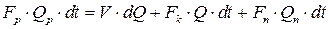 (6.51)
(6.51)
Для подальшого дослідження (6.51) слід врахувати, що:
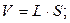 (6.52)
(6.52)
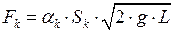 ; (6.53)
; (6.53)
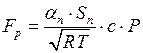 . (6.54)
. (6.54)
Схема випарної установки наведена на рис. 6.6.
Рис. 6.6. Випарна установка: 1 – підігрівач розчину; 2 - випарна установка; 3 – кип’ятильник.
Матеріальний баланс для рівня має вигляд:
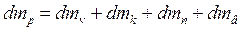 , (6.55)
, (6.55)
де 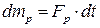 – масові витрати потоку рідини, що надходить до установки;
– масові витрати потоку рідини, що надходить до установки; 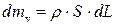 ;
; 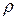 – густина рідини упареного розчину; S – поперечний перетин установки;
– густина рідини упареного розчину; S – поперечний перетин установки; 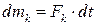 ;
; 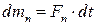 ;
; 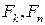 – масові витрати упареного розчину з куба і пари;
– масові витрати упареного розчину з куба і пари; 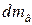 – кількість вторинної пари
– кількість вторинної пари
На підставі (6.52) – (6.55) рівняння матеріального балансу матиме вигляд:
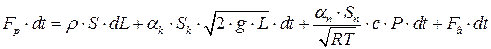 (6.56)
(6.56)
Для тиску рівня матеріального балансу можна записати:
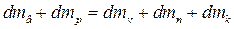 , (6.57)
, (6.57)
де 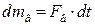 – маса речовини, що випаровується;
– маса речовини, що випаровується; 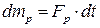 – маса свіжого розчину;
– маса свіжого розчину; 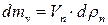 – маса парів в об’ємі;
– маса парів в об’ємі; 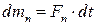 – маса парів, що відбирається з верхньої частини;
– маса парів, що відбирається з верхньої частини; 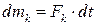 – маса випареного розчину, що призводить до зміни рівня рідини.
– маса випареного розчину, що призводить до зміни рівня рідини.
Звідки:
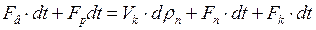 . (6.58)
. (6.58)
Враховуючи (6.52, а також що
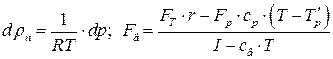 ; (6.59)
; (6.59)
де 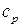 –питома теплоємність упареного розчину; Т – температура кипіння розчину.
–питома теплоємність упареного розчину; Т – температура кипіння розчину.
Тепловий баланс щодо температури випарної установки буде мати вигляд:
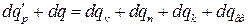 (6.60)
(6.60)
де 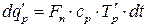 – теплота, що надходить із свіжим розчином;
– теплота, що надходить із свіжим розчином; 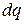 – теплота, що надходить з кип’ятильника 3, (рис. 6.6);
– теплота, що надходить з кип’ятильника 3, (рис. 6.6); 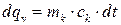 ;
; 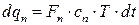 – теплота, що виходить з вторинною парою;
– теплота, що виходить з вторинною парою; 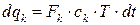 – теплота, що виходить з упареним розчином;
– теплота, що виходить з упареним розчином; 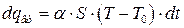 – теплота, що втрачається у навколишнє середовище.
– теплота, що втрачається у навколишнє середовище.
Свіжий розчин підігрівається в теплообміннику 1 (рис. 6.6). Кількість теплоти dqр знаходиться з системи рівнянь:
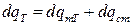 ; (6.61)
; (6.61)
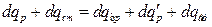 . (6.62)
. (6.62)
Для кип’ятильника (3) (Рис. 6.6) система рівнянь буде такою ж, проте кількість теплоти дорівнюватиме:
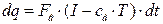 . (6.63)
. (6.63)

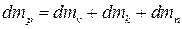 ; (6.48)
; (6.48)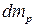 – маса цільового продукту, що надходить до установки;
– маса цільового продукту, що надходить до установки;  – маса цільового продукту, що накопичується в об’ємі V кубової частини;
– маса цільового продукту, що накопичується в об’ємі V кубової частини; 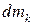 – маса продукту, що виходить з установки;
– маса продукту, що виходить з установки; 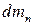 – маса продукту, що може витрачатися з вторинною парою.
– маса продукту, що може витрачатися з вторинною парою.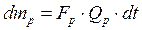 , (6.49)
, (6.49)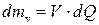 ,
, 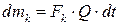
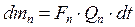 , (6.50)
, (6.50)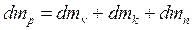 набуває вигляду:
набуває вигляду: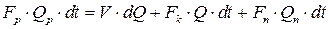 (6.51)
(6.51)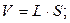 (6.52)
(6.52)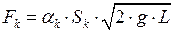 ; (6.53)
; (6.53)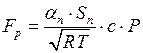 . (6.54)
. (6.54)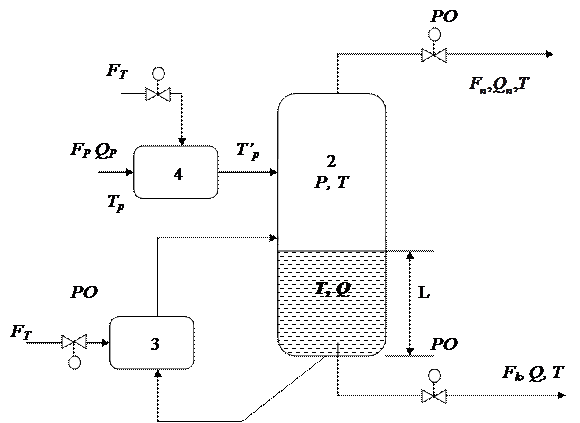
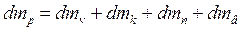 , (6.55)
, (6.55)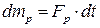 – масові витрати потоку рідини, що надходить до установки;
– масові витрати потоку рідини, що надходить до установки; 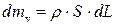 ;
; 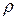 – густина рідини упареного розчину; S – поперечний перетин установки;
– густина рідини упареного розчину; S – поперечний перетин установки; 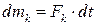 ;
; 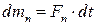 ;
; 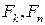 – масові витрати упареного розчину з куба і пари;
– масові витрати упареного розчину з куба і пари; 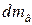 – кількість вторинної пари
– кількість вторинної пари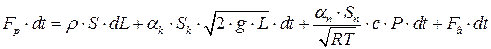 (6.56)
(6.56)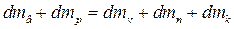 , (6.57)
, (6.57)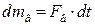 – маса речовини, що випаровується;
– маса речовини, що випаровується; 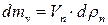 – маса парів в об’ємі;
– маса парів в об’ємі; 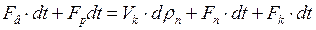 . (6.58)
. (6.58)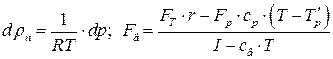 ; (6.59)
; (6.59)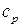 –питома теплоємність упареного розчину; Т – температура кипіння розчину.
–питома теплоємність упареного розчину; Т – температура кипіння розчину.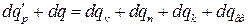 (6.60)
(6.60)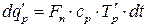 – теплота, що надходить із свіжим розчином;
– теплота, що надходить із свіжим розчином; 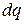 – теплота, що надходить з кип’ятильника 3, (рис. 6.6);
– теплота, що надходить з кип’ятильника 3, (рис. 6.6); 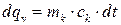 ;
; 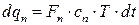 – теплота, що виходить з вторинною парою;
– теплота, що виходить з вторинною парою; 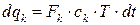 – теплота, що виходить з упареним розчином;
– теплота, що виходить з упареним розчином; 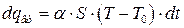 – теплота, що втрачається у навколишнє середовище.
– теплота, що втрачається у навколишнє середовище.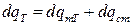 ; (6.61)
; (6.61)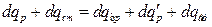 . (6.62)
. (6.62)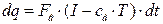 . (6.63)
. (6.63)


