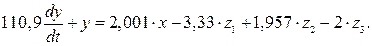Приклад 3. Побудова математичної моделі апарату з рідиною.
Розробити математичну модель апарату з рідиною, який має стік. В нормальному режимі роботи апарат характеризується параметрами: - висота рівня метаноло-водної суміші L=1,72 м; - кількість суміші в апараті m=1,8 т; - умовний прохідний діаметр стічного трубопроводу, на якому розміщується регулюючий орган, Dу=50 мм; - витрати приточного потоку Fn=24,1 м3/год; - температура приточного потоку t=60 - допустимі відхилення рівня L0=0,31 м. Вихідним параметром об’єкта керування є рівень рідини в апараті. До змінних параметрів відносяться витрати притоку Fn, висота рівня L, густина Незалежно від способу подачі рідини в апарат матеріальний баланс описується рівнянням:
де Тоді згідно з (4.157), враховуючи прирости змінних величин, рівняння (4.156) буде:
Після множення та нехтування складовими малої значущості матимемо:
Далі вилучимо рівняння статики:
Цей об’єкт відповідає такій структурно-логічній схемі, що наведена на рис.
Рис. Структурно-логічна схема об’єкту керування.
Тоді математична модель апарата з стоком матиме вигляд:
Наявність часу запізнення залежить від способу регулювання рівня. Якщо регулювання виконується за рахунок зміни витрат стоку, то запізнення відсутнє. У цьому разі передаточні функції становитимуть:
Знайдемо густину метаноло-водної суміші.
Беремо коефіцієнт витрат через регулюючий орган Поперечний перетин апарата Поперечний перетин регулюючого органу:
Об’єм суміші в апараті, який може змінюватись,
Стала часу об’єкта керування Коефіцієнти передачі об’єкта:
Тоді диференціальне рівняння, що описує об’єкт керування, матиме вигляд:
Передаточні функції об’єкта без ланки запізнення:
|

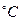 ;
;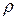 , поперечний перетин регулюючого органу
, поперечний перетин регулюючого органу 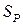 .
.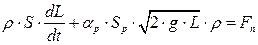 . Залежність густини від зміни температури має вигляд:
. Залежність густини від зміни температури має вигляд:
 – густина відповідно при температурі Т і Т 0;
– густина відповідно при температурі Т і Т 0; 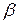 – коефіцієнт об’ємного розширення.
– коефіцієнт об’ємного розширення.

 . Матимемо:
. Матимемо: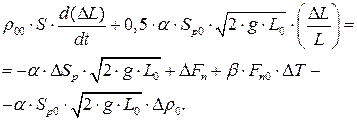 Введемо позначення
Введемо позначення 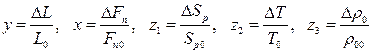 . Після їх підстановки в (4.161) і ділення на вираз
. Після їх підстановки в (4.161) і ділення на вираз 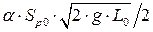 , матимемо:
, матимемо: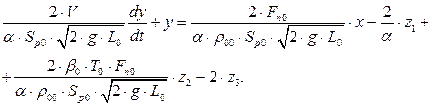 Введемо позначення
Введемо позначення 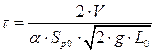 – стала часу;
– стала часу;
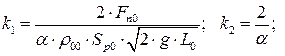

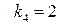 , – коефіцієнти передачі відповідно каналів x
, – коефіцієнти передачі відповідно каналів x  y, z 1
y, z 1 
 .
.
 кг/м3. де
кг/м3. де 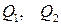 – доля метанолу та води;
– доля метанолу та води; 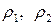 – їх густини при температурі 60
– їх густини при температурі 60 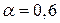 .
. м2.
м2. м2.
м2.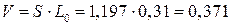 м3.
м3. с.
с.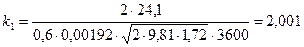 ;
; ;
; 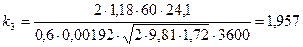 ;
;  .
.