Приклад 1. Отримання математичної моделі аналітичним методом для ресивера.
Отримати статичну модель аналітичним методом для ресивера. Розрахувати статичну модель Дані для розрахунку: Р 0 = 6 атм, Р = 4 атм, Р 1 = 2 атм, Визначаємо межі об’єкту моделювання, його вихід та входи. Відповідно заданій функціональній залежності Як розрахункову схему приймемо схематичне зображення об’єкта моделювання, представлене на рис.

Рис. Повітряний ресивер.
Таблиця. Початкові умови.
Таким чином, маємо ізотермічне розширення газу. Вхідною величиною є Складаємо рівняння матеріального балансу:
маємо:
Цей вираз є рівнянням статики, він пов’язує вихід
звідси:
Таким чином:
Підвівши до квадрату і здійснивши деякі перетворення отримаємо наступний вираз:
Тоді:
Для тиску
де,
Після підстановки даних з таблиці у рівняння (2.30) отримаємо:
Одержаний вираз і є рівнянням статичної моделі для ресивера у явній формі. Статична характеристика при
Статична характеристика повітряного ресивера зображена на рис.

Рис. Статична характеристика повітряного ресивера
Приклад 2. Побудова математичної моделі резервуару під тиском. Розробити математичну модель резервуару під тиском, якщо його об’єм становить Vр=10,0 м3, витрати повітря на вході Fn=5110 м3/год, коефіцієнт витрат регулюючого органу Матеріальний баланс об’єкту керування записується в вигляді:
Сталими параметрами нелінійної моделі є об’єм Vр резервуару, газова стала R, коефіцієнт витрати регулюючого органу До змінних параметрів відносяться: тиск Р в резервуарі, який є вихідним для об’єкту керування, температура газу Т, витрати газу Fn, площа поперечного перетину регулюючого органу SP. Структурно-логічна схема об’єкта керування зображена на малюнку рис. 4.19..
Рис. Структурно-логічна схема об’єкту керування.
Рівняння матеріального балансу запишемо в вигляді:
Підставляючи це рівняння в рівняння з відхиленнями, після множення та нехтування складовими малої ступені важливості, вилучення рівняння статики матимемо
Тоді, розділивши відповідне рівняння на
Позначимо
Тоді рівняння математичної моделі об’єкту матиме вигляд:
Сталу с знаходимо за формулою З рівняння статики знаходимо поперечний перетин регулюючого органу:
Знайдемо сталу часу об’єкту:
Сталу часу знайдено для випадку, коли тиск змінюється від 0,8 МПа до атмосферного. Враховуючи обмежуючі умови на відхилення величини тиску від номінального значення, стала часу буде меншою. Якщо, наприклад, у відповідності до технологічного процесу зміна тиску в резервуарі має бути 20% від номінального значення, стала часу буде Коефіцієнти передачі об’єкта будуть:
Рівняння математичної моделі матиме вигляд:
Передаточні функції щодо відповідних каналів впливу будуть:
Час запізнення об’єкта Час запізнення для такого об’єкта значно менший за сталу часу та для практичних розрахунків ним можна знехтувати.
|

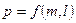 та побудувати статичну характеристику
та побудувати статичну характеристику 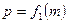 для повітряного ресивера.
для повітряного ресивера.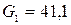 кг/г,
кг/г, 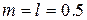 ,
,  .
.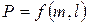 маємо одну вихідну величину Р та дві вхідні
маємо одну вихідну величину Р та дві вхідні 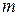 та
та  . Інші можливі входи, наприклад Р 0, Р 1, будуть незмінними і не розглядатимуться як входи. Виходячи з місць розташування вихідної величини Р та входів
. Інші можливі входи, наприклад Р 0, Р 1, будуть незмінними і не розглядатимуться як входи. Виходячи з місць розташування вихідної величини Р та входів 
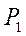



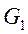
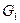
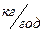
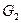

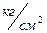
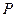
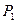
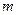

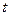

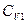
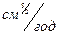
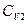
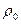
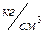
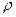

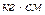
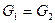 Враховуючи те, що:
Враховуючи те, що: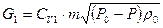

 .
. Оскільки:
Оскільки: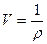 . то, маємо:
. то, маємо: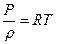
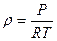 .
.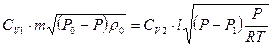 .
.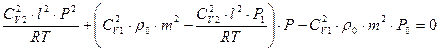
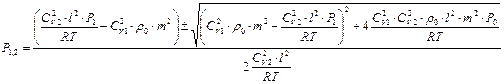
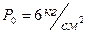 , температури
, температури 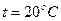 та щільностей повітря
та щільностей повітря 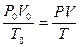 ;
; ;
; 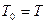 .
. ;
;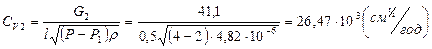 ;
; , см.
, см.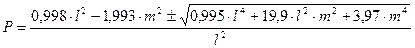
 буде мати наступний вигляд:
буде мати наступний вигляд: .
.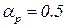 , тиск Р=0,8 МПа, температура t=25
, тиск Р=0,8 МПа, температура t=25  .
.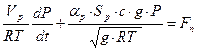 .
.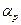 , стала с, яка залежить від показника адіабати для даного газу.
, стала с, яка залежить від показника адіабати для даного газу.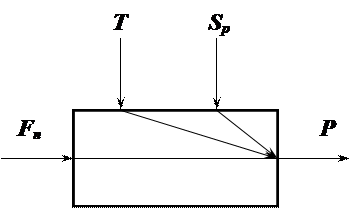
 . Змінні параметри:
. Змінні параметри: Функцію
Функцію 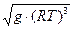 розкладемо в ряд Тейлора навколо номінального значення температури
розкладемо в ряд Тейлора навколо номінального значення температури 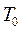 :
: . Рівняння статики
. Рівняння статики 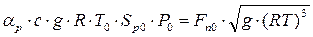 .
.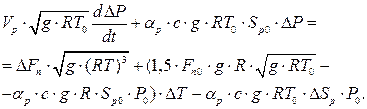 Приведемо це рівняння до відносних величин, вводячи позначення:
Приведемо це рівняння до відносних величин, вводячи позначення:
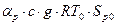 , матимемо:
, матимемо:
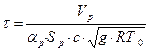 – стала часу;
– стала часу;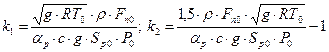 – коефіцієнти передачі.
– коефіцієнти передачі.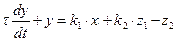 .
.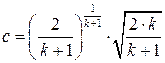 . Показник адіабати для двохатомних газів k=1,4 (в нашому випадку). Отже, с=0,684.
. Показник адіабати для двохатомних газів k=1,4 (в нашому випадку). Отже, с=0,684.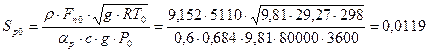 м2.
м2.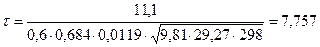 c.
c.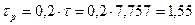 c.
c. ;
;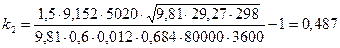 .
.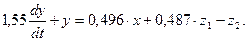
 .
.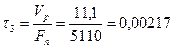 c.
c.


