Приклад 5. Побудова математичної моделі резервуару під тиском.
Розробити математичну модель резервуару під тиском, якщо його об’єм становить Vр=10,0 м3, витрати повітря на вході Fn=5110 м3/год, коефіцієнт витрат регулюючого органу Матеріальний баланс об’єкту керування записується в вигляді:
Сталими параметрами нелінійної моделі є об’єм Vр резервуару, газова стала R, коефіцієнт витрати регулюючого органу До змінних параметрів відносяться: тиск Р в резервуарі, який є вихідним для об’єкту керування, температура газу Т, витрати газу Fn, площа поперечного перетину регулюючого органу SP. Структурно-логічна схема об’єкта керування зображена на малюнку, рис.
Рис. Структурно-логічна схема об’єкту керування.
Це рівняння запишемо в вигляді:
Змінні параметри:
Рівняння статики Підставляючи відповідне рівняння, після множення та нехтування складовими малої ступені важливості, вилучення рівняння статики матимемо
Тоді, розділивши рівняння (4.104) на
Тоді рівняння математичної моделі об’єкту матиме вигляд:
Сталу с знаходимо за формулою З рівняння статики знаходимо поперечний перетин регулюючого органу:
Сталу часу знайдено для випадку, коли тиск змінюється від 0,8 МПа до атмосферного. Враховуючи обмежуючі умови на відхилення величини тиску від номінального значення, стала часу буде меншою. Якщо, наприклад, у відповідності до технологічного процесу зміна тиску в резервуарі має бути 20% від номінального значення, стала часу буде Коефіцієнти передачі об’єкта будуть:
Рівняння математичної моделі матиме вигляд:
Передаточні функції щодо відповідних каналів впливу будуть:
Час запізнення об’єкта Час запізнення для такого об’єкта значно менший за сталу часу та для практичних розрахунків ним можна знехтувати.
|

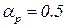 , тиск Р=0,8 МПа, температура t=25
, тиск Р=0,8 МПа, температура t=25 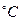 .
.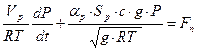 .
.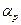 , стала с, яка залежить від показника адіабати для даного газу.
, стала с, яка залежить від показника адіабати для даного газу.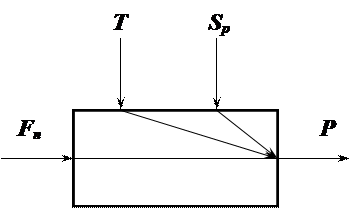
 .
. Функцію
Функцію 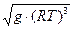 розкладемо в ряд Тейлора навколо номінального значення температури
розкладемо в ряд Тейлора навколо номінального значення температури 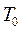 :
: .
.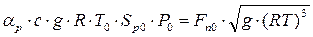 .
.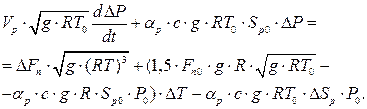 Приведемо це рівняння до відносних величин, вводячи позначення:
Приведемо це рівняння до відносних величин, вводячи позначення:
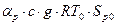 , матимемо:
, матимемо: Позначимо
Позначимо 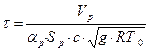 – стала часу;
– стала часу;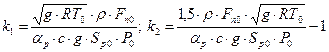 – коефіцієнти передачі.
– коефіцієнти передачі.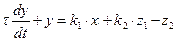 .
.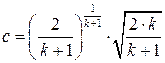 . Показник адіабати для двохатомних газів k=1,4 (в нашому випадку). Отже, с=0,684.
. Показник адіабати для двохатомних газів k=1,4 (в нашому випадку). Отже, с=0,684.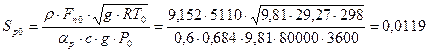 м2. Знайдемо сталу часу об’єкту:
м2. Знайдемо сталу часу об’єкту: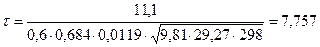 c.
c.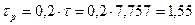 c.
c. ;
;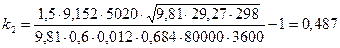 .
.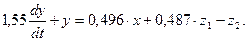
 .
.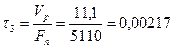 c.
c.


