Приклад 6. Побудова математичної моделі процесу переміщення рідин і газів
Розробити математичну модель об’єкту керування, що являє собою трубопровід, по якому протікає азотно-воднева суміш у співвідношенні 1:1,25. Витрати цієї суміші становлять Fn=250550 м3/год при температурі t=200 Густина азоту та водню знаходиться за формулою:
Нехай концентрація азоту В розрахунках приймаємо, що Тоді
Лінеаризуємо рівняння матеріального балансу:
Т – температура суміші; D – діаметр трубопроводу; L – довжина трубопроводу;
Змінними будуть
Підставивши ці вирази в (4.41), після почленного множення та нехтування складовими малої ваги, вилучення співвідношення статики, приведення до відносної форми, отримаємо наступне рівняння типу:
де
де Т 0 – номінальна температура. Знак “–” при k3, k4 показує, що зміна параметрів z2, z3 призводить до протилежної зміни y.
Знаходимо коефіцієнти передачі об’єкту
Обчислюємо сталу часу, коефіцієнти передачі, причому газова стала знаходиться за формулою:
Математична модель об’єкту в диференціальній формі має вигляд:
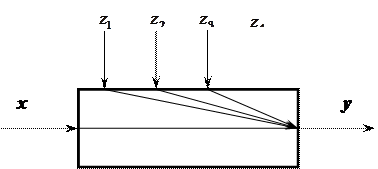
Ця модель відповідає такій структурно-логічній схемі рис.
Рис. Структурно-логічна схема об’єкту керування.
Час запізнення об’єкту визначається за формулою:
Кожний канал характеризується передаточною функцією, яка визначається з рівняння (2.8): для P для P для Р для Р Оскільки об’єкт керування має чисте запізнення, яке для всіх каналів береться однаковим, то передаточна функція трубопроводу як об’єкту керування становитиме послідовне з’єднання динамічної ланки та ланки запізнення, тобто:
Передаточні функції для каналів будуть:
|

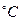 , тиску P=50МПа, діаметр трубопроводу D y =250мм, довжина L=20м. На вході об’єкту встановлено клапан для регулювання тиску (витрат) на його виході. В’язкість водню при t=200
, тиску P=50МПа, діаметр трубопроводу D y =250мм, довжина L=20м. На вході об’єкту встановлено клапан для регулювання тиску (витрат) на його виході. В’язкість водню при t=200  , азоту 0,0907
, азоту 0,0907 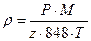 ,
,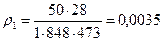
 – для азоту,
– для азоту,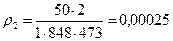
 В’язкість газової суміші становить:
В’язкість газової суміші становить: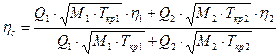 , де
, де  і
і 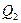 – відносні концентрації азоту та водню;
– відносні концентрації азоту та водню; і
і 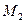 – молекулярна вага азоту та водню;
– молекулярна вага азоту та водню; і
і 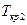 – критичні температури для азоту та водню;
– критичні температури для азоту та водню;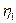 і
і 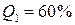 , водню
, водню  .
. ;
;  .
.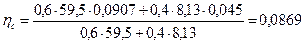
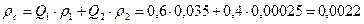 кг/м3.
кг/м3.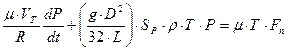 ,
,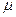 – в’язкість;
– в’язкість;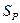 – поперечний перетин регулюючого органу;
– поперечний перетин регулюючого органу;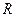 – газова стала;
– газова стала;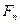 – витрати суміші;
– витрати суміші;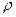 – густина.
– густина.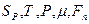 , причому:
, причому: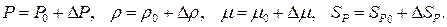
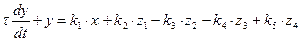 ,
, стала часу об’єкту;
стала часу об’єкту;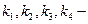 безрозмірні коефіцієнти передачі;
безрозмірні коефіцієнти передачі; – коефіцієнт передачі об’єкту за каналом
– коефіцієнт передачі об’єкту за каналом  ;
; – коефіцієнт передачі об’єкту за каналом
– коефіцієнт передачі об’єкту за каналом 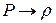 ;
;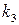 – коефіцієнт передачі об’єкту за каналом
– коефіцієнт передачі об’єкту за каналом 
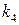 – коефіцієнт передачі об’єкту за каналом
– коефіцієнт передачі об’єкту за каналом 
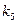 – коефіцієнт передачі об’єкту за каналом Р
– коефіцієнт передачі об’єкту за каналом Р  T.
T.
 c.
c.
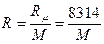 (RT має розмірність в метрах).
(RT має розмірність в метрах).


 c.
c. ;
;


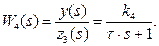
 , де
, де 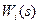 – передаточна функція і-того каналу;
– передаточна функція і-того каналу;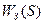 – передаточна функція ланки запізнення.
– передаточна функція ланки запізнення.



