Реактори
Реактори поділяються на газові і рідинні, на рис. 6.10
Рис. 6.10. Реактори: газовий (а) і рідинний (б)
Газові реактори, як правило, мають три вихідні величини: концентрацію цільового продукту, температуру і тиск. Газова суміш, яка надходить в реактор, попередньо нагрівається до температури Т г, близької до температури реакції. Реакції в газовому потоці (за невеликим винятком) відноситься до екзотермічних, тому реактор необхідно охолоджувати до деякої температури Т. Якщо газова суміш складається з двох потоків, то на вході в реактор вона містить два компоненти з концентраціями Q 1, Q 2. В результаті реакції між цими компонентами створюється нова речовина з концентрацією Q. Теплота, яка надходить у реактор, складається з теплоти газового потоку та теплоти, яка виділяється під час реакції. Рівняння теплового балансу газового реактору має вигляд:
де Коефіцієнт
де Рівняння матеріального балансу за реагуючим компонентом має вигляд:
де Якщо тиск Р у реакторі регулюється змінною витрат Fв газу на виході то:
де У рідинному реакторі рис. 6.10 (б) неперервної дії реагуючі потоки з витратами Рівняння теплового балансу має вигляд:
де Рівняння матеріального балансу реактору за концентрацією аналогічне (4.17й). Слід врахувати, шо
У реактор періодичної дії реагенти з масами
де Рівняння матеріального балансу має вигляд:
де З рівнянь матеріального та теплового балансів видно, що вони взаємопов’язані, тому такі об’єкти відносяться до об’єктів із взаємними сильними зв’язками. У кожному конкретному випадку математичну модель складають виходячи з конкретної задачі дослідження, враховуючи необхідну точність. Обмеження накладаються на подальші параметри та характеристики: технологічні параметри процесу; статичні характеристики об'єкту по досліджуваних каналах; залежність вихідного сигналу від лінійних координат (просторового положення); залежність вихідного сигналу від характеру внутрішніх зворотних зв’язків; втрати енергії; характеру обраної моделі (ідеального витіснення, змішування та ін.) До параметрів на які накладаються обмеження відносяться: коефіцієнт теплопровідності; в’язкість; теплоємність; коефіцієнти тепло- і масопередачі, коефіцієнти тепло- і масообміну. Коефіцієнт теплопровідності для газу (рівняння Сатерленда):
де Для рідини (формула Вебера):
де с – теплоємність; Для в’язкості газів:
де с – стала Сатерленда для в’язкості. Для рідин:
де А,В – сталі. Теплоємність:
де а, в, с – емпіричні коефіцієнти. Коефіцієнт тепловіддачі:
де
|


 , (6.80)
, (6.80) ;
;  – теплота, що виділяється в результаті реакції;
– теплота, що виділяється в результаті реакції;  ;
; 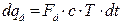 ;
;  – теплота, що передається через стінку до холодоносія;
– теплота, що передається через стінку до холодоносія;  – витрати газової суміші та її теплоємність; r– теплота реакції;
– витрати газової суміші та її теплоємність; r– теплота реакції;  – густина суміші у реакторі;
– густина суміші у реакторі;  – коефіцієнт теплопередачі через стінку; S – поверхня теплообміну; Тс – температура стінки.
– коефіцієнт теплопередачі через стінку; S – поверхня теплообміну; Тс – температура стінки. , (6.81)
, (6.81) – коефіцієнт пропорційності.
– коефіцієнт пропорційності. . (6.82)
. (6.82) ;
;  – маси реагуючих компонентів;
– маси реагуючих компонентів; 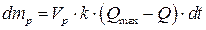 – кількість речовини, що створюється в процесі реакції;
– кількість речовини, що створюється в процесі реакції; 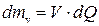 –кількість нової речовини у реакторі;
–кількість нової речовини у реакторі;  – кількість маси на виході реактора;
– кількість маси на виході реактора;  – об’єм реакційної зони;
– об’єм реакційної зони; 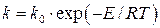 – стала швидкості реакції;
– стала швидкості реакції;  – стала величина;
– стала величина;  – енергія активації;
– енергія активації;  – універсальна газова стала; Т – температура;
– універсальна газова стала; Т – температура;  – максимально досяжна концентрація цільового продукту.
– максимально досяжна концентрація цільового продукту. . (6.83)
. (6.83)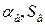 – коефіцієнт витраті прохідний отвір каналу.
– коефіцієнт витраті прохідний отвір каналу.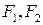 і концентраціями
і концентраціями  безпосередньо завантажуються у реактор з мішалкою. У об’ємі реакційної маси
безпосередньо завантажуються у реактор з мішалкою. У об’ємі реакційної маси 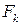 . Вважається, що реакція екзотермічна, і температура Т у реакторі підтримується за рахунок подачі холодоагенту у оболонку.
. Вважається, що реакція екзотермічна, і температура Т у реакторі підтримується за рахунок подачі холодоагенту у оболонку. . (6.84)
. (6.84) ;
;  ;
;  ;
;  ;
; 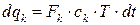 ;
;  – втрати теплоти з газами;
– втрати теплоти з газами;  – теплота, що віддається теплоносієві;
– теплота, що віддається теплоносієві; 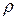 – густина реакційної маси;
– густина реакційної маси;  – маса і теплоємність реакційної речовини.
– маса і теплоємність реакційної речовини. (6.85)
(6.85) завантажуються, після чого створюються умови для реакції (наприклад, підвищення температури). Якщо реакція екзотермічна, то після досягнення температури реакції, теплоносій відключається і в оболонку реактора подається холодоносій для забезпечення сталості температури реакції. Тобто процес регулювання температури у реакторі здійснюється зміною витрати холодоносія
завантажуються, після чого створюються умови для реакції (наприклад, підвищення температури). Якщо реакція екзотермічна, то після досягнення температури реакції, теплоносій відключається і в оболонку реактора подається холодоносій для забезпечення сталості температури реакції. Тобто процес регулювання температури у реакторі здійснюється зміною витрати холодоносія 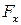 . Тобто рівняння теплового балансу реактора буде:
. Тобто рівняння теплового балансу реактора буде: (6.86)
(6.86) ;
;  ;
;  ;
; 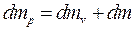 , (6.87)
, (6.87) ;
; 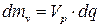 ;
; 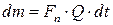 ;
; 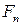 – масова швидкість перемішування.
– масова швидкість перемішування. , (6.88)
, (6.88)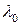 – коефіцієнт теплопровідності при 0 °С; Т – температура; с – стала Сатерленда для теплопровідності.
– коефіцієнт теплопровідності при 0 °С; Т – температура; с – стала Сатерленда для теплопровідності. . (6.89)
. (6.89) , (6.90)
, (6.90) . (6.91)
. (6.91) . (6.92)
. (6.92) . (4.181)
. (4.181) – витрата;
– витрата;  – діаметр труби;
– діаметр труби; 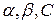 – сталі коефіцієнти.
– сталі коефіцієнти.


