Введение. по асимптотическим методам в теории
Курсовая работа по асимптотическим методам в теории дифференциальных уравнений
Выполнил: студентка группы ММ-09-01 Когут Я.П.
Проверил: профессор кафедры дифференциальных уравнений Остапенко В.А.
г. Днепропетровск 2011 г. Содержание Введение………………………………………………………………………3 Теоретическая часть …………...…………………………………………...4 Раздел 1. Система Ляпунова ─ случай одной степени свободы………….......4 1. Система Ляпунова.…………………………………………….4 2. Приведение к каноническому виду. …………………………4 3. Преобразование интеграла H. ………………………………..5 4. Периодичность решений системы Ляпунова. ………………5 5. Теорема Ляпунова. ……………………………………………7 Раздел 2. Условия существования периодических решений.…………..…..10 1. Необходимые и достаточные условия периодичности. …….10 Раздел 3. Метод Ляпунова. ………………………………………………………13 1. Алгоритм. ……………………………………………………..13 Практическая часть ……………………………………………………….16 Список литературы ………………………………………………………..17 Введение. Метод Ляпунова ─ Пуанкаре посвящен изложению основ классической теории периодических решений дифференциальных уравнений, правые части которых являются аналитическими функциями своих переменных. Эта теория возникла из работ Ляпунова и Пуанкаре в конце 19 века и в последующие десятилетия получила дальнейшее развитие. В ней появились новые точки зрения, расширился круг изучаемых вопросов. Наряду с исследованиями теоретического характера продолжилась дальнейшая разработка методов эффективного построения периодических решений. Начиная с двадцатых годов прошлого века, теория Ляпунова ─ Пуанкаре благодаря работам Андронова и Мандельштама находит широкое применение в теории колебаний. Большой вклад в дальнейшее развитие классической теории периодических решений сделали И. Г. Малкин и Г. В. Каменков. В этой курсовой работе будет рассматриваться алгоритм построения периодического решения задачи Коши системы дифференциальных уравнений
Теоретическая часть Раздел 1. Система Ляпунова ─ случай одной степени свободы.
Система Ляпунова. Рассмотрим систему дифференциальных уравнений
где
Систему (1.1) будем называть системой Ляпунова, если выполняются следующие условия: 1) уравнение
имеет чисто мнимые корни 2) система (1.1) допускает аналитический первый интеграл
разложение которого по степеням переменных
|

 (1.1)
(1.1) и
и 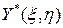 ─ аналитические функции своих переменных в окрестности точки
─ аналитические функции своих переменных в окрестности точки 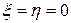 и такие, что их разложение по степеням
и такие, что их разложение по степеням  и
и  начинается с членов, порядок которых не ниже второго:
начинается с членов, порядок которых не ниже второго: (1.2)
(1.2)
 (1.3)
(1.3)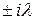 ;
;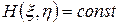 , (1.4)
, (1.4) в окрестности точки
в окрестности точки