Приведение к каноническому виду.Рассмотрим вспомогательную систему уравнений Система (1.5) описывает колебание с постоянной амплитудой, поскольку её характеристическое имеет пару чисто мнимых корней. Исключая из уравнения (1.5) переменную
Для того, чтобы удовлетворилось условие 1), коэффициент при
Сделаем замену
где Таким образом, получим
Как мы видим при помощи замены (1.7) уравнение (1.6) сводится к эквивалентной системе двух уравнений
Также
Поэтому, если в исходной системе (1.1) сделать замену (1.7), то эта система будет приведена к виду (1.8).
где
|
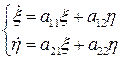(1.5)
, получим
(1.6)
должен быть равен нулю, т. е. должно быть 
и, кроме того, должно иметь место неравенство
.
, 
, (1.7)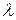
─ арифметическое значение корня 
.
.
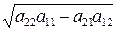(1.7’)
(1.8) – система Ляпунова в каноническом виде
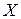и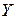 
─ аналитические функции своих переменных, разложение которых начинается с членов второго порядка малости. Таким образом, вместо системы (1.1) нам достаточно рассмотреть систему (1.8).
