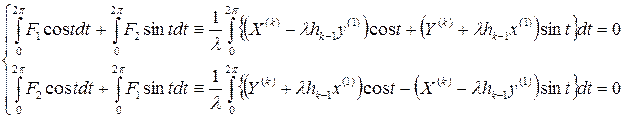Алгоритм. Ляпунов предложил простой и очень эффективный метод построения периодических решений для достаточно малых значений постоянной с решения системы (1.8)
Ляпунов предложил простой и очень эффективный метод построения периодических решений для достаточно малых значений постоянной с решения системы (1.8). Алгоритм Ляпунова использует аналитичность искомых решений по параметру с и дает правило построения решений в форме рядов специального вида, разложенных по степеням этого параметра. Таким образом, на основании теоремы в разделе 1, решение системы уравнений (1.8) можно искать в виде:
но это невозможно, так как период решения Т неизвестен. Тогда Ляпунов предложил видоизменить масштаб времени так, чтобы решения полученной системы имели фиксированный период, не зависящий от с (например, равный Обратим внимание на формулу (1.24). Она показывает, что если ввести замену
то период колебаний по переменной
Так как правые части системы (3.2) мы умножили на аналитические функции параметра Периодические решения системы (3.2) будем искать в виде рядов
Подставим ряды (3.3) в систему уравнений (3.2) и сравним коэффициенты при одинаковых степенях параметра
В самом деле, функции
Следовательно, функции
Функции
где Точно так же каждая пара функций
причем функции Кроме того, функции
и т. д. Из уравнений (1.13) следует, что функции
Вернемся снова к уравнениям (3.2). Хотя числа Далее члены рядов (3.3) также определяются однозначно, причём
Так как функции
Таким образом, мы можем утверждать заранее, что функции
где являются периодическими функциями времени, поскольку они определяются периодическими функциями
На этом основании можно сформулировать следующее вспомогательное утверждение: функции
Практическая часть
Индивидуальное задание
Список литературы. 1. Моисеев Н. Н. Асимптотические методы нелинейной механики, Наука, М., 1981 г. 2. Малкин И. Г. Некоторые задачи теории нелинейных колебаний, ГИТТЛ, М., 1956.
|

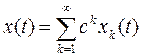 ,
, 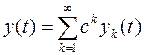 .
.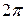 ).
).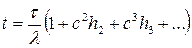 (3.1)
(3.1) будет равен
будет равен  (3.2)
(3.2)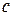 , то решение этой системы, так же как и системы (1.8), аналитические по
, то решение этой системы, так же как и системы (1.8), аналитические по 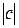 периодические по
периодические по  ,
, 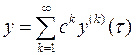 . (3.3)
. (3.3)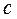 . Функции
. Функции  и
и 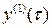 будут удовлетворять следующей системе уравнений:
будут удовлетворять следующей системе уравнений: ,
, 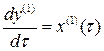 . (3.4)
. (3.4)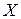 и
и 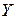 , будучи аналитическими функциями своих переменных, таковы, что их разложение начинается с членов второго порядка малости. Следовательно, при подстановке в эти функции рядов (3.3) функции
, будучи аналитическими функциями своих переменных, таковы, что их разложение начинается с членов второго порядка малости. Следовательно, при подстановке в эти функции рядов (3.3) функции 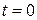 :
:  ,
,  .
.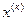 и
и 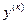 будут соответствовать следующим начальным условиям:
будут соответствовать следующим начальным условиям: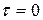 :
:  ,
,  ,
,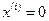 ,
,  , где i =2,3… (3.5)
, где i =2,3… (3.5)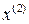 и
и  будут удовлетворять системе уравнений
будут удовлетворять системе уравнений (3.6)
(3.6)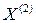 и
и 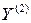 ─ квадратичные члены разложения функций
─ квадратичные члены разложения функций  и
и 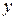 , причем их разложение начинается с квадратичных членов, то
, причем их разложение начинается с квадратичных членов, то 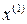 и
и 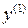 .
.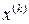 и
и 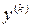 , входящая в разложение (3.3), определяется системой уравнений
, входящая в разложение (3.3), определяется системой уравнений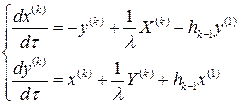 (3.7)
(3.7) и
и 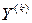 будут содержать величины
будут содержать величины  и
и  только тех номеров
только тех номеров  , которые меньше чем
, которые меньше чем  .
.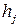 , причем
, причем 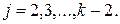 Заметим, что величины
Заметим, что величины 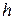 входят в правые части (3.7) только уравнений относительно
входят в правые части (3.7) только уравнений относительно  и
и  , для которых
, для которых 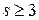 :
: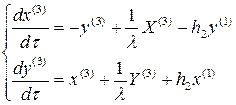 (3.8)
(3.8) удовлетворяют начальным условиям
удовлетворяют начальным условиям ,
,  . (3.9)
. (3.9) нам неизвестны заранее, но они на основании теоремы Ляпунова определяются однозначно для данной системы и не зависят от параметра
нам неизвестны заранее, но они на основании теоремы Ляпунова определяются однозначно для данной системы и не зависят от параметра 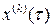 и
и 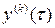 ─ периодические функции переменного
─ периодические функции переменного 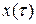 и
и  ─ периодические функции, следовательно,
─ периодические функции, следовательно, (3.10)
(3.10) ,
,  .
.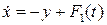 ,
,  , (2.11)
, (2.11) ,
, 
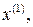 …,
…, 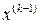 ,
,  . Система вида (2.11) имеет периодическое решение тогда и только тогда, когда функции
. Система вида (2.11) имеет периодическое решение тогда и только тогда, когда функции 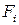 удовлетворяют условиям
удовлетворяют условиям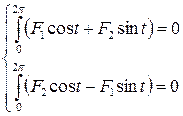
 всегда удовлетворяют условиям (3.11)
всегда удовлетворяют условиям (3.11)