Преобразование интеграла H.
Остановимся ещё на выражении интеграла
где Но сначала рассмотрим ситуацию, когда первый интеграл имеет вид:
Так как (1.9) ─ первый интеграл, то вдоль каждой кривой семейства (1.8) он должен обращаться в 0. Тоесть
Подставим и получим
Сравнивая коэффициенты при При y: При х: При ху: При х2: При у2: Отсюда Итак, интеграл H можно представить в виде
где Таким образом, мы видим, что представление первого интеграла всегда имеет вид (*) и, кроме того, его можно представить в виде (1.10)
|

 . Согласно положению 2) его представление имеет вид
. Согласно положению 2) его представление имеет вид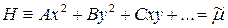 , (*)
, (*)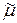 ─ некоторая постоянная.
─ некоторая постоянная.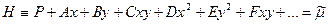 (1.9)
(1.9)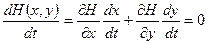 .
.
 ,
,  и
и  , получим
, получим

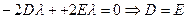

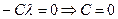
 =
= 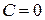 , D=E. Не нарушая общности можно принять
, D=E. Не нарушая общности можно принять 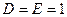 .
.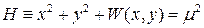 , (1.10)
, (1.10)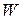 ─ аналитическая функция своих переменных, разложение которой начинается с членов не ниже третьего порядка малости,
─ аналитическая функция своих переменных, разложение которой начинается с членов не ниже третьего порядка малости,  ─ некоторая постоянная, которую всегда мы можем считать положительной для достаточно малых
─ некоторая постоянная, которую всегда мы можем считать положительной для достаточно малых  и
и  .
.


