Докажем теперь, что существует периодическое решения системы (1.8) для достаточно малых значений 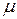 . И что это решение ─ периодические функции
. И что это решение ─ периодические функции 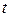 . Для этого достаточно доказать, что фазовые траектории в плоскости
. Для этого достаточно доказать, что фазовые траектории в плоскости  замкнутые и
замкнутые и 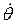 сохраняет знак. Для этого введём полярные координаты
сохраняет знак. Для этого введём полярные координаты
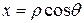 ;
; 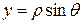
и заметим, что любая замкнутая траектория 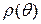 должна быть периодической функцией аргумента
должна быть периодической функцией аргумента 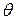 . Составим выражение для
. Составим выражение для  :
:
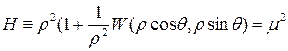 (1.11)
(1.11)
Здесь 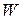 ─ аналитическая функция
─ аналитическая функция 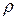 , разложение которой имеет вид
, разложение которой имеет вид
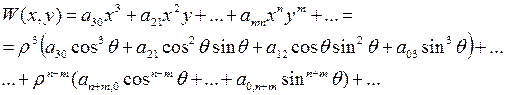
Следовательно, в формуле (1.11) функция  может быть представлена в виде ряда
может быть представлена в виде ряда
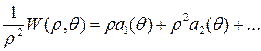 ,
,
причем, все коэффициенты 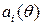 ─ полиномы от
─ полиномы от 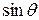 и
и 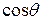 , т. е. периодические функции
, т. е. периодические функции 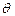 . Таким образом, выражение (1.11) можно переписать так:
. Таким образом, выражение (1.11) можно переписать так:
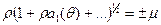
Это равенство мы можем рассматривать как уравнение для определения 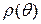 .
.
Используя аналитичность функций, которые в него входят, будем функцию 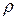 разыскивать в виде ряда
разыскивать в виде ряда
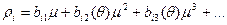 , i =1, 2. (1.12)
, i =1, 2. (1.12)
Прямым вычислением убеждаемся в том, что коэффициенты в разложении (1.12) являются полиномами от 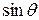 и
и 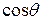 . Так, например,
. Так, например,
 ,
, 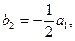
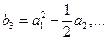
Таким образом, коэффициенты 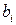 ─ степенные функции коэффициентов
─ степенные функции коэффициентов 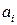 , а последние в свою очередь являются полиномами от
, а последние в свою очередь являются полиномами от 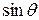 и
и 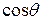 . Вследствие такой структуры коэффициентов ряд (1.12) определяет периодическую функцию
. Вследствие такой структуры коэффициентов ряд (1.12) определяет периодическую функцию 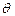 периода
периода 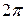 , т. е. при изменении
, т. е. при изменении 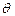 на
на 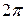 величина
величина 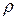 возвращается к своему исходному значению. Если при этом окажется, что
возвращается к своему исходному значению. Если при этом окажется, что 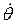 сохраняет знак, то это и будет означать, что фазовая траектория замкнутая.
сохраняет знак, то это и будет означать, что фазовая траектория замкнутая.
Таким образом, решения системы (1.8) ─ функции 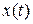 и
и 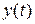 ─ будут периодическими функциями времени.
─ будут периодическими функциями времени.
Функции 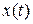 и
и 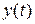 являются аналитическими по параметру
являются аналитическими по параметру 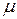 . В самом деле, в силу аналитичности правых частей системы (1.8) её решения будут аналитическими функциями начальных значений
. В самом деле, в силу аналитичности правых частей системы (1.8) её решения будут аналитическими функциями начальных значений
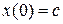 ,
, 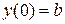 .
.
Постоянная 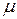 так же определяется этими значениями
так же определяется этими значениями
 . (1.13)
. (1.13)
Так как правые части системы (1.8) не зависят от времени, то без ограничений общности начальные условия можно записать в виде
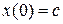 ,
, 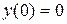 . (1.14)
. (1.14)
Отсюда видно, что решения системы (1.8) представляют собой аналитические функции 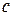 .
.

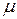 . И что это решение ─ периодические функции
. И что это решение ─ периодические функции 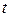 . Для этого достаточно доказать, что фазовые траектории в плоскости
. Для этого достаточно доказать, что фазовые траектории в плоскости  замкнутые и
замкнутые и 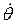 сохраняет знак. Для этого введём полярные координаты
сохраняет знак. Для этого введём полярные координаты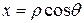 ;
; 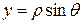
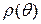 должна быть периодической функцией аргумента
должна быть периодической функцией аргумента 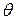 . Составим выражение для
. Составим выражение для  :
: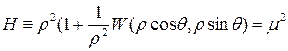 (1.11)
(1.11) ─ аналитическая функция
─ аналитическая функция 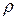 , разложение которой имеет вид
, разложение которой имеет вид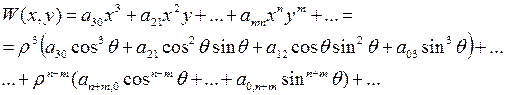
 может быть представлена в виде ряда
может быть представлена в виде ряда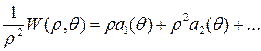 ,
,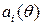 ─ полиномы от
─ полиномы от  и
и  , т. е. периодические функции
, т. е. периодические функции 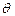 . Таким образом, выражение (1.11) можно переписать так:
. Таким образом, выражение (1.11) можно переписать так: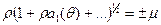
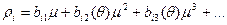 , i =1, 2. (1.12)
, i =1, 2. (1.12) ,
, 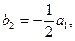
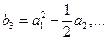
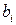 ─ степенные функции коэффициентов
─ степенные функции коэффициентов 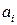 , а последние в свою очередь являются полиномами от
, а последние в свою очередь являются полиномами от 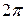 , т. е. при изменении
, т. е. при изменении 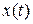 и
и 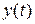 ─ будут периодическими функциями времени.
─ будут периодическими функциями времени.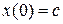 ,
, 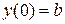 .
. . (1.13)
. (1.13)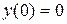 . (1.14)
. (1.14)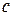 .
.


