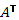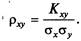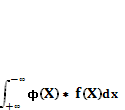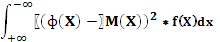Многомерное нормальное распределение и его числовые характеристики.
23. Числовые характеристики линейных преобразований случайного вектора. Этот вопрос состоит не в перечислении числовых характеристик (их всего 4: Математическое ожидание, дисперсия, корреляционный момент (ковариация) и коэффециент корреляции) А в перечислении способов вычисления этих характеристик. Линейная функция — функция вида Y=kx+b Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности. Свойства · · При · При · При · · При
В случае со случайными векторами линейный закон записывается: Y=AX+C – Связь X с Y посредством линейного преобразования Где A – матрица неслучайных элементов C – Константа. Мат. Ож находится так: M(Y) = M(AX+C) = A* M(X)+C Дисперсия находится:
Корреляционный момент (ковариация) так: K(Y) = A*K(X)* Коэффициент корреляции:
24. Числовые характеристики нелинейных преобразований случайного вектора. Здесь для вычисления числовых характеристик вектора Y нужно знать закон совместного распределения X.
Пусть Y = ф(X), а f(X) – плотность распределения вероятности для X Тогда: M(Y) = D(Y) =
|
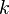является тангенсом угла, который образует прямая с положительным направлением оси абсцисс.
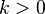, прямая образует острый угол с осью абсцисс.
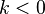, прямая образует тупой угол с осью абсцисс.
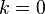, прямая параллельна оси абсцисс.
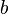является показателем ординаты точки пересечения прямой с осью ординат.
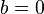, прямая проходит через начало координат.
