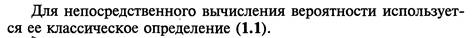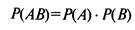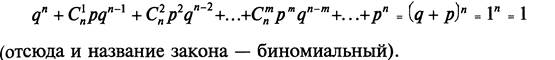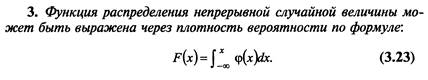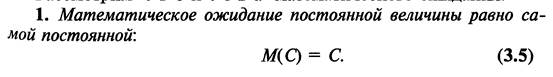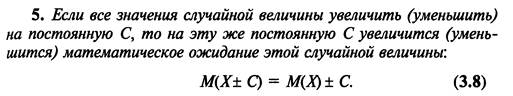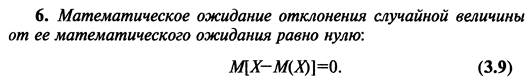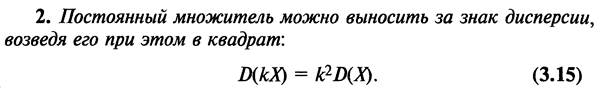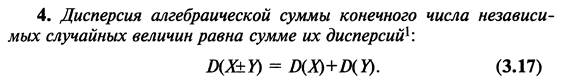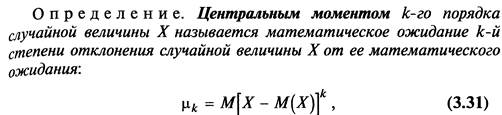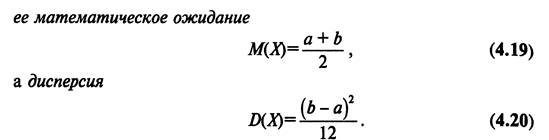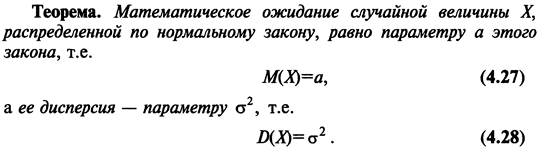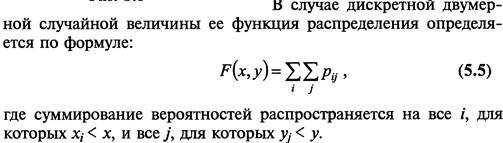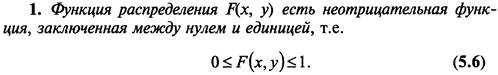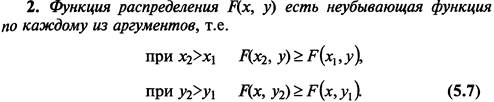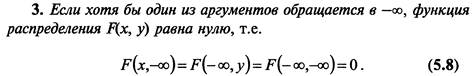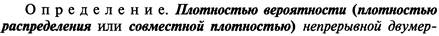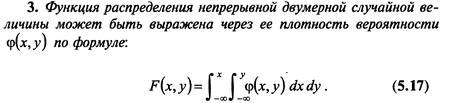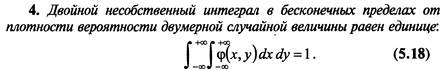Случайные события. Непосредственный подсчет вероятности событий.

 

 

2. Статическое определение вероятности. Понятие о сходимости по вероятности.

Применяется, когда события не равновозможные.

Сходимость по вероятности:

Для любого E>0

(Т.е, чем больше опытов, тем больше вероятность того, что относительная частота будет меньше отличаться от вероятности. Но только ВЕРОЯТНОСТЬ)

Так же:

Сходимость по вероятности. Последовательность случайных величин X₁, X₂,... сходится по вероятности к случайной величине X, если для любого ε > 0 вероятность неравенства | Х_n—Х|<ε при n→∞ стремится к единице.

Этим подчёркивается то,что сходимость по вероятности отличается от сходимости алгебраической.

 

 

3. События зависимые и независимые. Теорема умножения вероятностей.

 

Следствие 2:

Если события А и В независимы, то ф-ла принимает след вид:

Следствие 3:

 

 

4. Теорема сложения вероятностей. События совместные и несовместные.

Для 3х событий формула принимает след. вид: P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(CB)+P(ABC)

 

5. Формула полной вероятности. Теорема гипотез Бейеса.

6. Распределение дискретной случайной величины. Биномиальный закон.

7. Функция распределения вероятностей и ее свойства.

 

8. Плотность распределения вероятностей и ее свойства.

9. Математическое ожидание и его свойства.

 

10. Дисперсия и ее свойства.

 

 

 

 

11. Начальные и центральные моменты. Ассиметрия эксцесс.

 

 

 

 

12. Равномерный закон распределения вероятностей и его числовые характеристики.

 

13. Нормальный закон распределения вероятностей и его числовые характеристики.

 

14. Функция Лапласа и ее свойства.

 

 

 

15. Понятие о локальной и интегральной теоремах Лапласа.

 

 

16. Функции распределения вероятностей случайного вектора и ее свойства.

Св-ва аналогичны св-вам фии распределения одномерной сл вел:

 

17. Плотность распределения случайного вектора и ее свойства.

Св-ва аналогичны св-вам плотности вероятности одномерной сл вел: