Проверка гипотез о математическом ожидании нормальной генеральной совокупности.
На практике иногда оказывается, что средний результат одной серии наблюдений заметно отличается от среднего результата другой серии. Что это? Влияние ошибок наблюдения? Или, может быть, мы имеем дело с двумя разными генеральными совокупностями. Итак, имеем две случайные величины Х и У. Обе подчиняются нормальному закону распределения. Допустим, что мы располагаем двумя независимыми выборками объёмами n1 и n2 соответственно. Нулевая гипотеза: М (Х)= М (У). За альтернативную гипотезу примем Если гипотеза Н 0 справедлива, то разность их арифметических средних Введём нормированную случайную величину критическое значение для Приведём пример. Допустим, что мы располагаем двумя сериями наблюдений с количеством n 1 =25 и n2 =50. При этом, получены средние значения Вычислим нормированную разность
Из таблицы функции Лапласа следует, что c вероятностью (надёжностью) 0,99 наша нормированная случайная величина должна быть меньше 2,576. Область значений z>2,576 при нашей гипотезе достичь практически невозможно. Это означает, наблюдаемое расхождение нельзя считать случайным. Следует отметить, что в случае z<2,576, ещё нельзя утверждать, что гипотеза подтвердилась. С помощью проверки гипотез можно лишь отвергнуть проверяемую гипотезу, но никогда нельзя доказать её справедливость.
|

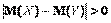 . Дисперсии этих двух выборок будем считать известными.
. Дисперсии этих двух выборок будем считать известными.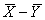 распределена также по нормальному закону, а дисперсия этой разности (при условии, что Х и У – независимы!) равна сумме дисперсий этих случайных переменных:
распределена также по нормальному закону, а дисперсия этой разности (при условии, что Х и У – независимы!) равна сумме дисперсий этих случайных переменных: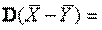
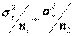 .
. , которая также распределенанормально и имеет дисперсию¸ равную единице, и математическое ожидание, равное нулю. С помощью таблицы, функции Лапласа, нетрудно установить
, которая также распределенанормально и имеет дисперсию¸ равную единице, и математическое ожидание, равное нулю. С помощью таблицы, функции Лапласа, нетрудно установить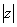 , которое наша разность не может превосходить с заданной вероятностью
, которое наша разность не может превосходить с заданной вероятностью 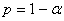 . Если гипотеза Н0 имеет место, то эта вероятность мало отличается от единицы. Чем меньше
. Если гипотеза Н0 имеет место, то эта вероятность мало отличается от единицы. Чем меньше 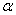 , тем меньше вероятность отклонить проверяемую гипотезу.
, тем меньше вероятность отклонить проверяемую гипотезу.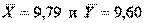 . Установить с вероятностью 0,99, является ли это расхождение случайным. Пусть обе случайные величины имеют стандартное отклонение
. Установить с вероятностью 0,99, является ли это расхождение случайным. Пусть обе случайные величины имеют стандартное отклонение 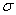 = 0, 30.
= 0, 30.




