Рассмотрим две случайные величины Х и У, каждая из которых подчиняется нормальному закону с дисперсиями 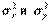 . Пусть из этих генеральных совокупностей извлечены две выборки объёмами п1 и п2. Проверим гипотезу Н0 о том, что
. Пусть из этих генеральных совокупностей извлечены две выборки объёмами п1 и п2. Проверим гипотезу Н0 о том, что 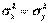 относительно альтернативной гипотезы Н1, заключающейся в том, что
относительно альтернативной гипотезы Н1, заключающейся в том, что 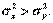
Однако, мы располагаем только выборочными дисперсиями 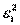 =
= 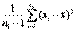 и
и 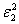 =
=  . Задача проверки гипотезы Н0 сводится к сравнению выборочных дисперсий.
. Задача проверки гипотезы Н0 сводится к сравнению выборочных дисперсий.
Для построения критической области с выбранной надёжностью необходимо исследовать совместный закон распределения оценок 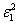 и
и 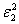 . Таким законом распределения является распределение Фишера – Снедекора (или F - распределение)
. Таким законом распределения является распределение Фишера – Снедекора (или F - распределение)
Рассмотрим случайную величину 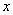 , распределённую нормально с математическим ожиданием Х и с дисперсией
, распределённую нормально с математическим ожиданием Х и с дисперсией  . Произведём две независимые выборки объёмами п1 и п2. Для оценки
. Произведём две независимые выборки объёмами п1 и п2. Для оценки  используют выборочные дисперсии. Случайную величину, определяемую отношением
используют выборочные дисперсии. Случайную величину, определяемую отношением 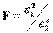 , называют величиной с распределением Фишера-Снедекора. Имеются таблицы для дифференциального закона распределения Фишера-Снедекора, которые зависят лишь от объёма выборки и уровня значимости
, называют величиной с распределением Фишера-Снедекора. Имеются таблицы для дифференциального закона распределения Фишера-Снедекора, которые зависят лишь от объёма выборки и уровня значимости
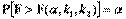 , где k1 = n1 -1, k2 = n2 -1.
, где k1 = n1 -1, k2 = n2 -1.
Вернёмся снова к задаче проверки гипотезы о равенстве дисперсий. Сначала нужно вычислить выборочные дисперсии. Найдём отношение F= 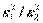 ,причём в числителе поставим большую из двух оценок дисперсии. Выберем уровень значимости
,причём в числителе поставим большую из двух оценок дисперсии. Выберем уровень значимости 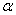 и из таблиц находим число F
и из таблиц находим число F 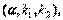 которое сравнивается с вычисленным F. Если окажется, что
которое сравнивается с вычисленным F. Если окажется, что  , то проверяема гипотеза Н0 отвергается, в противном случае делается вывод о том, что наблюдения не противоречат проверяемой гипотезе.
, то проверяема гипотеза Н0 отвергается, в противном случае делается вывод о том, что наблюдения не противоречат проверяемой гипотезе.

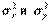 . Пусть из этих генеральных совокупностей извлечены две выборки объёмами п1 и п2. Проверим гипотезу Н0 о том, что
. Пусть из этих генеральных совокупностей извлечены две выборки объёмами п1 и п2. Проверим гипотезу Н0 о том, что 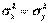 относительно альтернативной гипотезы Н1, заключающейся в том, что
относительно альтернативной гипотезы Н1, заключающейся в том, что 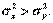
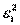 =
= 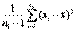 и
и 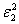 =
=  . Задача проверки гипотезы Н0 сводится к сравнению выборочных дисперсий.
. Задача проверки гипотезы Н0 сводится к сравнению выборочных дисперсий.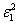 и
и 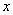 , распределённую нормально с математическим ожиданием Х и с дисперсией
, распределённую нормально с математическим ожиданием Х и с дисперсией  . Произведём две независимые выборки объёмами п1 и п2. Для оценки
. Произведём две независимые выборки объёмами п1 и п2. Для оценки 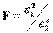 , называют величиной с распределением Фишера-Снедекора. Имеются таблицы для дифференциального закона распределения Фишера-Снедекора, которые зависят лишь от объёма выборки и уровня значимости
, называют величиной с распределением Фишера-Снедекора. Имеются таблицы для дифференциального закона распределения Фишера-Снедекора, которые зависят лишь от объёма выборки и уровня значимости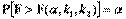 , где k1 = n1 -1, k2 = n2 -1.
, где k1 = n1 -1, k2 = n2 -1.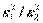 ,причём в числителе поставим большую из двух оценок дисперсии. Выберем уровень значимости
,причём в числителе поставим большую из двух оценок дисперсии. Выберем уровень значимости 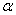 и из таблиц находим число F
и из таблиц находим число F 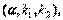 которое сравнивается с вычисленным F. Если окажется, что
которое сравнивается с вычисленным F. Если окажется, что  , то проверяема гипотеза Н0 отвергается, в противном случае делается вывод о том, что наблюдения не противоречат проверяемой гипотезе.
, то проверяема гипотеза Н0 отвергается, в противном случае делается вывод о том, что наблюдения не противоречат проверяемой гипотезе.


