ПРИЛОЖЕНИЕ. ИЗУЧЕНИЕ НОНИУСОВ
Часто при измерении длины какого-либо тела длина его не укладывается в целое число делений масштаба. Для того чтобы можно было поручиться при линейных измерениях и за десятые доли масштаба (а иногда и за сотые), пользуются нониусом. Нониус – это дополнительная шкала к основному масштабу (линейному или круговому), позволяющая повысит точность измерения с данным масштабом в 10,20 и более число раз. Нониусы бывают линейные и круговые, прямые и обратные, нерастянутые и растянутые. Линейный нониус представляет собой небольшую линейку (шкалу), скользящую вдоль большей масштабной линейки (рис. 1).
Длина отрезка, измеряемая при помощи нониуса, будет равна числу целых делений масштаба до нуля нониуса плюс точность нониуса, умноженная на номер его деления, совпадающего с некоторым делением масштаба. На рис. 2 длина тела равна 13 – ти целым и 3-м десятых, так как совпадает с делениями масштаба 3 – е деление нониуса. Погрешность, которая может возникнуть при таком методе отсчета, будет обуславливаться неточным совпадение деления нониуса с одним из делений масштаба, и величина ее не будет превышать, очевидно,
В обратном нониусе длина одного деления нониуса больше длины одного деления масштаба на величину точности нониуса. Техника измерения с обратным нониусом такая же, что и с прямым, с той лишь разницей, что обратный нониус прикладывается к концу измеряемого отрезка таким образом, чтобы числа делений нониуса убывали в сторону возрастания делений основного масштаба. Чтобы легче было заметить, какое деление нониуса совпадает с каким- либо делением основной шкалы, на практике делают нониусы растянутыми. Прямой растянутый нониус получится, если длина одного деления нониуса будет короче не одного наименьшего деления масштаба (как мы полагали до сих пор), а двух, трех и т.д. наименьших делений его. Точность нониуса в этом случае определяется по той же формуле.
|

 Как видно из рис.1, 10 делений нониуса соответствуют 9 делениям основного масштаба. В случае прямого нерастянутого нониуса, который мы рассматриваем, одно деление нониуса короче одного деления масштаба на величину Δ, которая называется точностью нониуса. Точность нониуса Δ является разностью длин делений основного масштаба и нониуса и легко может быть определена, если мы знаем число делений нониуса n и длину наименьшего деления масштаба αm
Как видно из рис.1, 10 делений нониуса соответствуют 9 делениям основного масштаба. В случае прямого нерастянутого нониуса, который мы рассматриваем, одно деление нониуса короче одного деления масштаба на величину Δ, которая называется точностью нониуса. Точность нониуса Δ является разностью длин делений основного масштаба и нониуса и легко может быть определена, если мы знаем число делений нониуса n и длину наименьшего деления масштаба αm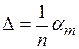 .
.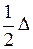 .
. Таким образом, можно сказать, что погрешность нониуса равна половине его точности.
Таким образом, можно сказать, что погрешность нониуса равна половине его точности.


