Пример 5.11.
Имеется следующий портфель из трех облигаций:
В этом примере суммарная рыночная стоимость портфеля равна 57 350 000 евро, k = 3. Расчет доли рыночной стоимости отдельных видов облигаций в портфеле показан ниже:
Средневзвешенная доходность портфеля тогда будет равна: 0,1606×0,092 + 0,3505×0,101 + 0,4889×0,085 = 0,0917 или 9,17 %. В то время как это – наиболее часто используемая мера доходности портфеля, средняя доходность предоставляет очень мало информации о потенциальной доходности портфеля. Чтобы в этом убедиться, представим, что у нас есть портфель из двух облигаций: шестимесячной облигации, которая предлагает доходность к погашению 11%, и 30-летняя облигация, которая предлагает доходность к погашению 8%. Предположим, 99% портфеля инвестировано в шестимесячную облигацию, и 1% - в тридцатилетнюю облигацию. Средневзвешенная доходность портфеля будет равна 10,97%. Но что значит эта доходность? Как ее можно использовать в дельнейшем анализе активов и обязательств? Портфель практически весь состоит из шестимесячной облигации, хотя там и есть 30-летняя облигация. Сможет ли менеджер банка уверенно предлагать по двухлетним депозитным вкладам доходность 9% в год? Это на целых 1,97% меньше доходности портфеля, если использовать средневзвешенную доходность портфеля. Это было бы неверно, потому что доходность портфеля последующие два года будет целиком опираться на процентные ставки периода, который начинается через шесть месяцев от настоящего момента.
|
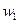= 9 210 000 / 57 350 000 = 0,1606
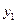= 0,092
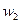= 20 100 000 / 57 350 000 = 0,3505
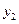= 0,101
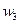= 28 040 000 / 57 350 000 = 0,4889
