Стоки и источники на плоскости
Вводя удельный расход
Интегрируя (2.17), находим
Получили очень важную формулу потенциала точечного стока на плоскости. Как видим, потенциал в окрестности скважины пропорционален логарифму расстояния r от скважины. Точечным стоком называют скважину бесконечно малого радиуса, хотя в природе такой скважины не существует. В гидродинамике эксплуатационную скважину принимают за точечный сток (q >0), а нагнетательную – за точечный источник (q <0) и называют их соответственно: скважина-сток и скважина-источник. Исследуем (2.17) и (2.18). При r =0 значения Ф и Итак, плоские задачи фильтрации эффективно могут быть решены с помощью потенциала. Пусть на плоскости известны потенциалы Ф к и Ф с на двух концентрично расположенных окружностях с радиусами R к и r с (рис. 2.4).
Рис. 2.4. Схемы притока к стоку (источнику) на плоскости Согласно (2.18) имеем:
откуда следует:
Переходя от потенциала к давлению в (2.19), получим формулу Дюпюи (2.10).
|

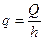 и учитывая, что ds =- dr, получаем следующее выражение для скорости фильтрации
и учитывая, что ds =- dr, получаем следующее выражение для скорости фильтрации (2.17)
(2.17)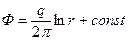 . (2.18)
. (2.18) обращаются в
обращаются в  ¥; при r= ¥ значение Ф =¥, а
¥; при r= ¥ значение Ф =¥, а 
 ,
, ,
,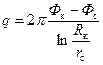 . (2.19)
. (2.19)


