Связь теории функции комплексного переменного с плоской задачей теории фильтрации. Функция тока. Комплексный потенциал
Для плоского движения несжимаемой жидкости потенциал является функцией двух координат, т. е. Ф = Ф (х, у). Уравнения движения записываются в виде:
Уравнение неразрывности есть
Уравнение Лапласа
Найдем уравнение линий тока. Линией тока называется такая линия, касательная к которой в любой точке совпадает с вектором скорости. Отсюда следует выражение для направляющих косинусов (рис. 3.1):
или
откуда следует уравнение линий тока
Здесь ds – элемент линии тока с проекциями dх и dу,
α; и β; – углы между осями координат и вектором скорости Решение уравнения (3.4) будем искать в виде неявной зависимости
Уравнение (3.5) называется функцией тока. Основное свойство функции тока — это ее постоянство вдоль линии тока. Но с переходом от одной линии тока к другой значение функции тока y (х, у) меняется (рис. 3.2).
Установим связь функции тока с потенциалом скорости фильтрации Ф (х, у)= С. Поскольку y (х, у)= const вдоль линии тока. то полный дифференциал ее равен нулю, т. е.
Это то же уравнение линий тока, что и (3.23), но только в неявной форме. Сравнивая (3.6) и (3.3), получаем:
Сравнивая (3.1) и (3.7), находим:
или
Получили уравнения Коши-Римана, удовлетворяющие уравнению Лапласа.
|

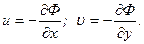 (3.1)
(3.1) (3.2)
(3.2) (3.3)
(3.3)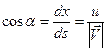


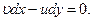 (3.4)
(3.4)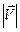 – модуль вектора скорости с проекциями u и
– модуль вектора скорости с проекциями u и  ;
;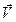 .
. (3.5)
(3.5)
 (3.6)
(3.6)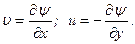 (3.7)
(3.7)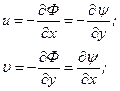
 (3.8)
(3.8)


