В пласте с прямолинейным контуром питания
Если бы пласт был неограниченным и в нем была бы единственная скважина, то потенциал любой точки определялся бы формулой (3.9) при п =1, т. е.
При r = r c потенциал Ф с на контуре скважины является величиной постоянной (Ф с= сonst). Следовательно, формула (3.11) условиям на контуре скважины удовлетворяет. Условиям на контуре питания (ось х, см. рис. 3.6) эта формула не удовлетворяет, т. к. она дает переменные значения потенциала Ф, поскольку радиус r принимает произвольные значения по оси х. При помощи метода отражения мы можем добиться выполнения условия постоянства потенциала на контуре питания (Ф к= const). Пусть С 1 есть зеркальное отражение скважины С (рис. 3.5). Тогда для любой точки М пласта, согласно формуле (3.11), можем записать выражение для результирующего потенциала
где q 1 и q 2 – удельные дебиты скважины–стока (С) и скважины–источника (С 1). Но так как q 1=- q 2, то
Формула (3.12) удовлетворяет условиям на контуре питания, т.к. при r1= r 2 (на оси х) потенциал принимает постоянное значение Ф=С=Ф к. Учитывая последнее, запишем формулу (3.12) в виде
Чтобы найти неизвестный удельный дебит, перенесем току М (см. рис. 3.5) на контур действительной скважины. Тогда по принципу суперпозиции получим
откуда находим
Формула Дюпюи для плоскорадиального притока, как известно, записывается в виде
Сравнивая формулы (3.14) и (3.15), видим, что дебиты будут одинаковы, если R к=2 а. Этот факт дал возможность В.Н. Щелкачеву сделать вывод, что в естественных условиях контур питания не является идеальной геометрической линией (прямой или окружностью), а принимает некоторое промежуточное положение Мп (рис. 3.8).
Рис. 3.7. Схема к определению влияния формы контура
|

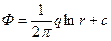 . (3.11)
. (3.11)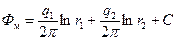 ,
,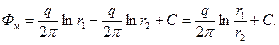 (3.12)
(3.12)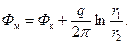 (3.13)
(3.13)
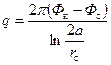 . (3.14)
. (3.14) . (3.15)
. (3.15)



