Стационарная фильтрация упругой капельной жидкости в недеформируемой пористой среде
Установим зависимость объемного веса от давления, т. е. g=g (P). Очевидно, для сжимаемой жидкости при увеличении давления на dP объемный вес повышается на dg. В дифференциальной форме это запишется в виде
где К 0=10¸20 тыс. атм. — модуль упругости сжатия жидкости. К 0 является переменной величиной и зависит от давления. Зависимость g=g (P) в небольшом диапазоне изменения давления можно аппроксимировать как линейную, параболическую и экспоненциальную. Полагая К 0= сonst и интегрируя (4.9), получаем:
где g 0 и g соответствуют начальному Р 0 и текущему Р давлениям. Исключая постоянную, получаем
или
Здесь Таким образом, установили, что объемный вес жидкости в зависимости от давления изменяется по экспоненциальному закону. Разложим функцию (4.10) в ряд Маклорена:
Удерживая первые два члена разложения, находим
Перепишем (4.11) в другой форме:
Как видим, в приближенной постановке зависимость g=g (P) удовлетворяет закону Гука. Пользуясь формулами (4.10) и (4.11), найдем точное и приближенное значение функции Лейбензона:
или
Обычно для капельной жидкости величина
Нетрудно заметить, что формула (4.15) может быть получена также интегрированием (4.6) при Отсюда следует вывод, что если жидкость малосжимаема, т. е. g»g 0= const, и сжимаемостью можно пренебречь, то при обычных значениях К 0 и (P – P 0) стационарное движение сжимаемой жидкости можно рассчитывать по формулам для несжимаемой жидкости объемного веса g 0. При этом погрешность в определении весового расхода будет определяться третьим членом в разложении Маклорена.
|

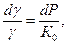 (4.9)
(4.9)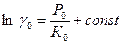 ;
; ,
,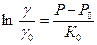
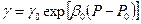 . (4.10)
. (4.10) — коэффициент сжимаемости жидкости.
— коэффициент сжимаемости жидкости.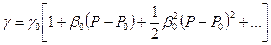 .
.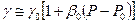 . (4.11)
. (4.11) . (4.12)
. (4.12)
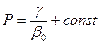 ; (4.13)
; (4.13)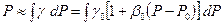 . (4.14)
. (4.14) . Тогда можно приближенно записать
. Тогда можно приближенно записать . (4.15)
. (4.15)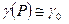 (
(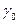 соответствует начальному давлению P 0).
соответствует начальному давлению P 0).


