Несжимаемой жидкости и газа к галерее
В соответствии с аналогией между стационарной фильтрацией сжимаемой и несжимаемой жидкости весовой расход газа G запишется формулой
Подставляя значение функции Лейбензона (4.20) в (4.21), получаем
Объемный расход газа Q пр, приведенный к атмосферным условиям, определится формулой
Как известно, при фильтрации несжимаемой жидкости давление распределяется по линейному закону (см. рис. 4.1). По аналогии для притока сжимаемой жидкости имеем
Подставив значение функции Лейбензона (4.20) в (4.24), получаем
Как видим, функция Лейбензона или квадрат абсолютного давления вдоль газового пласта, при притоке к галерее, распределяется по линейному закону (см. рис. 4.1). Распределение давления, как это следует из (4.25), выражается параболической зависимостью
На рис. 4.2 представлено распределение давления для несжимаемой жидкости и газа при P к=100 ат, P г=0.
Рис. 4.2. Распределение давления вдоль пласта при прямолинейном протоке несжимаемой жидкости и газа 4.3.2. Приток к совершенной скважине; распределение давления. В соответствии с указанной аналогией преобразуем формулу Дюпюи для притока газа к скважине. Получаем
Объемный расход Q пр, приведенный к атмосферным условиям согласно (4.20), выразится формулой
Распределение функции Лейбензона по радиусу кругового пласта будет аналогично распределению давления при притоке несжимаемой жидкости, т. е.
Подставляя (4.20) в (4.29), получаем
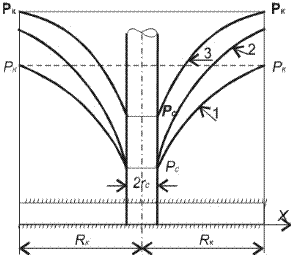
Выражения (4.29) и (4.30) представляют собой уравнения логарифмических кривых, вращение которых образуют «воронку депрессии» (рис. 4.3). Из формулы (4.30) следует функция распределения давления в пласте
Рис. 4.3. «Воронки депрессии» в случае притока жидкости
|

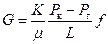 . (4.21)
. (4.21) . (4.22)
. (4.22)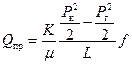 . (4.23)
. (4.23)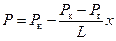 . (4.24)
. (4.24)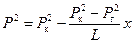 . (4.25)
. (4.25) . (4.26)
. (4.26)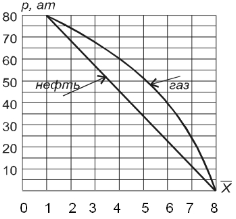
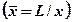
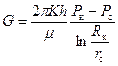 (4.27)
(4.27)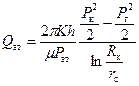 . (4.28)
. (4.28) . (4.29)
. (4.29) . (4.30)
. (4.30)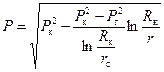 . (4.31)
. (4.31)