Одномерное установившееся движение сжимаемой жидкости и газа в трубке тока переменного сечения. Функция Лейбензона
Предположим, что фильтрация сжимаемой жидкости происходит по закону Дарси в трубке тока переменного сечения f (s) (см. рис. 1.5) при изотермическом движении (Т = const). Пусть вязкость жидкости является функцией давления, а проницаемость – функцией давления и положения точки, т. е.
Зависимости (4.1) определяются по опытным данным [5]. Пренебрегая проекцией массовой силы на направление движения и учитывая, что весовой расход G жидкости или газа при установившемся движении в любом сечении остается постоянным, можно записать
Введем обобщенную функцию давления
Тогда закон фильтрации (4.2) запишется в виде
Сравнивая (4.4) и (1.22), устанавливаем аналогию между стационарным движением несжимаемой и сжимаемой жидкости: аналогом объемного расхода Q несжимаемой жидкости является весовой расход G сжимаемой жидкости; аналогом напора Н – функции Р *, аналогом коэффициента фильтрации С – функция проницаемости K 1(Р), аналогом объемной скорости u – весовая скорость (g u). Пользуясь указанной аналогией, все решения, формулы и выводы для несжимаемой жидкости можно применить для случая стационарного движения сжимаемой жидкости или газа[5]. При K 2(P)= сonst и m (P)= сonst из (4.3) следует
Здесь Р представляет функцию Лейбензона
В этом случае уравнение (4.4) интегрируется сразу после введения функции Лейбензона. В общем же случае требуется численное интегрирование. Аналогичным образом можно ввести функцию Лейбензона и для массового расхода
Нелинейный закон фильтрации выражается степенными формулами или двучленной формулой вида
Аналогичным образом можно ввести обобщенную функцию Р * или, при m=сonst и К = сonst, функцию Лейбензона.
|

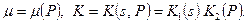 (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3)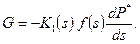 (4.4)
(4.4)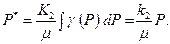 (4.5)
(4.5) (4.6)
(4.6)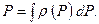 (4.7)
(4.7)
 (4.8)
(4.8)


