Взаимодействии совершенных скважин
Здесь п – число стоков на плоскости; i =1, 2, 3... п; ri — расстояние точки М до i- го стока; Qi – дебит i -гo стока; h –толщина пласта. В центрах стоков (ri =0) и на бесконечности (ri =¥) получаем бесконечный потенциал (Ф м=¥). В отличие от потенциалов скорости течения, вызванные отдельнымстоками, складываются векторно.
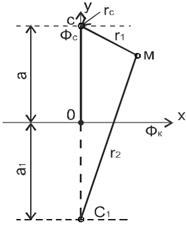
3.2.2. Приток к совершенной скважине в пласте с прямолинейным контуром питания. Метод отражения. Покажем применение формулы (3.9) для решения задачи о притоке несжимаемой жидкости к одиночной скважине радиуса r c в полосообразном полубесконечном пласте (рис 3.5) с прямолинейным контуром питания, где поддерживается постоянное давление Р к или потенциал Ф к. Для простоты схему выберем так,чтобы ось х проходила через прямолинейную границу пласта, а ось у – через выбранную скважину–сток. Схеме рис. 3.6, например, соответствует схема полосообразной полубесконечной залежи (рис. 3.7) с прямолинейным контуром питания, на котором известны давление Р к и проекция единичной скважины радиусом r c с забойным давлением Р с.
Рис. 3. 5. Схема к методу отражения скважины-стока в
|