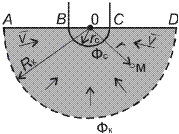
Стоки и источники в пространстве
Рассмотрим задачу о потенциале точечного стока в пространстве. В этом случае приток будет радиально-сферический (рис. 2.5). По закону Дарси имеем
С другой стороны, можно записать
где f =4 pr 2 – площадь фильтрации сферы. Приравнивая указанные выражения и интегрируя, получаем
Рис. 2.5. Схема радиально-сферического притока Получили формулу потенциала точечного стока в пространстве. При r= 0 имеем Ф =-¥, u =¥; при r= ¥ получаем Ф = const, u =0. Покажем использование формулы (2.20). Пусть Ф к и Ф с потенциалы на сферах, описанных радиусами R к и r с. Согласно (2.20) имеем:
По правилу производных пропорций из (2.21) имеем
При r ®¥ const в (2.20) становится потенциалом на бесконечности. Обычно Тогда
Таким образом, для точечного стока в пространстве радиус контура питания
Рис. 2.6. Схема радиально-сферического притока в полупространстве (скважина вскрыла лишь кровлю пласта)
|

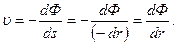

 (2.20)
(2.20)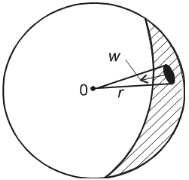
 (2.21)
(2.21) . (2.22)
. (2.22)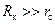 , следовательно,
, следовательно, 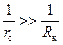 .
. . (2.23)
. (2.23)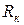 практически на дебит не влияет. В случае плоскорадиального притока (формула Дюпюи) ошибка в выборе
практически на дебит не влияет. В случае плоскорадиального притока (формула Дюпюи) ошибка в выборе  . (2.24)
. (2.24)