Дифференциальные уравнения теории установившейся фильтрации однородно жидкости
Для характеристки неустановившегося движения (т. е. когда скорости фильтрации, дебиты меняются со временем) оказывается необходимым использовать методы математической физики, основанные на составлении и интегрировании дифференциальных уравнений. При фильтрации однородной жидкости неизвестными функциями являются: 1) давление Р в любой точке пористой среды; 2) плотность r жидкости; 3) вектор скорости фильтрации 4) т – пористость; 5) температура среды Т ср; 6) температура жидкости Т ж. Таким образом, имеем 8 неизвестных функций. Но ввиду малых скоростей фильтрации в пласте движение остается практически изотермическим, поэтому число неизвестных сокращается до шести. Итак, мы установили шесть неизвестных функций. Перейдем к их выводу. Введем уравнение фильтрации как обобщение закона Дарси, который в векторной форме, как это было показано раньше, имеет вид [5-8]:
При такой записи массовыми силами для сжимаемой жидкости пренебрегаем. Уравнение неразрывности (сплошности) фильтрации жидкости в пористой среде записывается в виде:
Для сплошного потока жидкости, например в трубе, т = 0, имеем:
Здесь
Выражение (1.42) представляет собой уравнения движения жидкости в пористой среде. Чтобы система уравнений была замкнутой, необходимо добавить уравнение состояния.
При изотермическом процессе (Т=const) имеем: для несжимаемой жидкости
для упругой жидкости
для реальных газов
где Z – коэффициент сжимаемости (для идеальных газов Z =1); R – газовая постоянная; T – температура пласта; ρ,ρ;0 – плотности, соответствующие значениям давлений Р и Р 0; К 0 – модуль упругости жидкости. Проницаемость является функцией давления. т = т (P). (1.47) Считают, что для реальных пластов изменение пористости подчиня- ется закону Гука
где К с – модуль упругости пористой среды. Заметим, что запись потенциала Ф в уравнениях (1.39) и (1.42) справедлива, если К – const и m=const. В этом случае для несжимаемой жидкости (r=const) в неизменяемой пористой среде (т=const) уравнение неразрывности будет иметь вид
Тогда, подставляя (1.42) в (1.49), получаем:
Получили одно из важнейших уравнений математической физики – уравнение Лапласа. Стационарное распределение температуры, стационарное движение электричества удовлетворяют уравнению Лапласа. Электромоделирование основано на использовании этого уравнения. При этом аналогом давления является электрический потенциал. Оказывается, если заданы одинаковые граничные условия и дифференциальные уравнения имеют одинаковый вид, то, изучая процесс на какой-либо другой модели, можно получить решение, справедливое для процессов из другой области. Потенциал скорости фильтрации, очевидно, удовлетворяет уравнению Лапласа
Уравнение Лапласа является линейным, а для последних справедлив принцип суперпозиции, т. е. сумма частных решений линейных уравнений, умноженных на произвольные постоянные, также является решением этого линейного дифференциального уравнения. Математически это выглядит так. Если имеется несколько фильтрационных потоков Ф 1, Ф 2, Ф 3,..., Фп,которые удовлетворяют уравнению Лапласа, т. е,
то суммарный потенциал Ф =
Итак, потенциалы отдельных фильтрационных потоков несжимаемой жидкости складываются алгебраически, а векторы скорости фильтрации – геометрически.
|

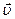 , представленный 3-мя компонентами по координатным осям;
, представленный 3-мя компонентами по координатным осям;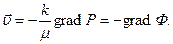 (1.39)
(1.39)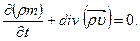 (1.40)
(1.40)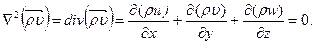 (1.41)
(1.41)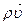 – вектор массовой скорости фильтрации. Если спроектировать вектор скорости фильтрации
– вектор массовой скорости фильтрации. Если спроектировать вектор скорости фильтрации 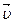 на координатные оси, то модули составляющих векторов запишутся в виде:
на координатные оси, то модули составляющих векторов запишутся в виде: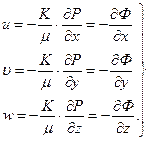
 (1.42)
(1.42)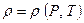 . (1.43)
. (1.43)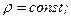 (1.44)
(1.44)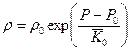 ; (1.45)
; (1.45)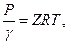 (1.46)
(1.46)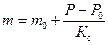 , (1.48)
, (1.48)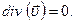 (1.49)
(1.49)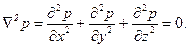 (1.50)
(1.50)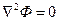 . (1.51)
. (1.51)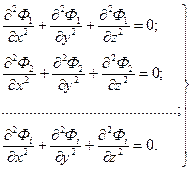 (1.52)
(1.52)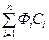 также удовлетворяет уравнению Лапласа, т. е
также удовлетворяет уравнению Лапласа, т. е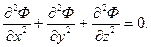 (1.53)
(1.53)


