Геометрические характеристики пористой среды
Пористость. Пористость понимается как общая и как эффективная. Коэффициент общей пористости – это отношение объема всех пор (V п) к общему объему образца (V 0), т. е.
Коэффициент эффективной пористости – это отношение сообщающихся между собой пор (V пc) к объему образца (V 0), т. е.
На практике в промысловых условиях используют такую характеристику как средняя пористость продуктивного пласта по всей залежи или по отдельному участку, которая определяется по следующим формулам. Среднеарифметический коэффициент пористости
Коэффициент пористости, средневзвешенный по площади h 1,
Коэффициент пористости, средневзвешенный по объему,
Коэффициент пористости, средневзвешенный по площади Аi,
Здесь i= 1, 2, 3 ,..., п –число скважин, в которых определялась пористость тем или иным методом (по керновому анализу, по данным гидродинамических и геофизических исследований и т. д.). Наиболее точным из указанных методов считается метод определения коэффициента пористости, средневзвешенного по объему. Коэффициент динамической пористости определяется формулой
Удельная поверхность – это отношение площади внутренних поверхностей (F)пор к единице объема материала (V), т. е.
Ясно, что для материалов с мелкозернистой структурой удельная поверхность намного больше, чем для материалов с крупнозернистой структурой. Этот параметр является весьма важным при характеристике способности пористой среды пропускать через себя жидкости и газы. В количественном отношении удельная поверхность – величина значительная. Так, удельная поверхность в 1 м3 песка составляет S =10 тыс. м2. Эффективный диаметр частицы грунта. В определении размера пор удобной мерой был бы диаметр пор. Однако этот термин имеет геометрический смысл только для среды, поры которой сферической формы, чего в природе не существует. Были попытки представить пористую среду, сложенную из трубок, параллельных друг другу. Эта попытка также не дала эффекта. Наиболее подходящей характеристикой среды оказался так называемый эффективный диаметр частиц, который определяется механическим анализом. В результате получают кривую фракционного состава (рис. 1.2), по которой и определяют средний эффективный диаметр частиц, используя формулу
где di –средний диаметр i фракции; п –число частиц фракции. Этот диаметр является важной, но не исчерпывающей характеристикой, поскольку он дает представление только о размере зерна, но не учитывает шероховатости, схему укладки, извилистость и т. д.
Рис. 1.2. Кривая механического анализа естественного грунта (W –весовое количество фракций зерен диаметра di ) Извилистость является в большей степени кинематической характеристикой, которая представляет относительную среднюю длину пути, пройденного жидкой частицей от стенки к стенке в поровом пространстве. Однако и этот параметр остается под сомнением. Характерный размер l пористой среды или масштаб породы, который определяется приближенно как
где
1.2. Скорость фильтрации. Истинная или действительная средняя скорость движения частицы Рассмотрим модель пористой среды пласта или так называемую трубку тока (рис. 1.3), площадь поперечного сечения которой f, давления на концах модели Р 1 и Р 2. Пусть Р 1> Р 2. Под действием разности давлений D Р = Р 1– Р 2 жидкость начинает двигаться. Однако жидкость будет двигаться не через всю площадь сечения f, а только через площадь просветов f пр, которую называют живым сечением потока. Исходя из теории статистики, можно считать, что в любом сечении трубки f пр будет иметь одинаковое значение.
Рис. 1.3. Модель пористой среды пласта (трубка тока постоянного сечения )
Если Q –объемный расход жидкости через модель с перепадом давления D Р, тогда скорость фильтрации u определяется из соотношения
Очевидно, скорость фильтрации не является действительной средней скоростью движения в живом сечении. Последняя будет больше скорости фильтрации и и определится из соотношения
Установим связь между u и u. Пусть dx –расстояние между двумя сечениями, dt –время, за которое жидкость из одного сечения переместилась в другое. Объем жидкости, вытесненной из области dx, можно определить из соотношения dV=Qdt=mfdx. Отсюда следует:
Подставляя (1.11), (1.12) в (1.13), получим
|

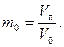 (1.1)
(1.1)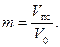 (1.2)
(1.2)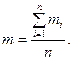 (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5)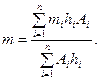 (1.6)
(1.6)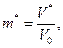 (1.7)
(1.7) –объем пор, где имеет место фильтрация.
–объем пор, где имеет место фильтрация.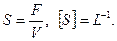 (1.8)
(1.8)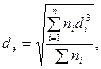 (1.9)
(1.9)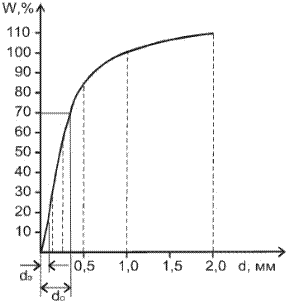
 (1.10)
(1.10)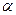 – коэффициент, зависящий от структуры пористой среды, извилистости и т. д. Методы определения и измерения указанных геометрических характеристик описываются в курсе физики плата.
– коэффициент, зависящий от структуры пористой среды, извилистости и т. д. Методы определения и измерения указанных геометрических характеристик описываются в курсе физики плата.
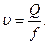 (1.11)
(1.11) (1.12)
(1.12)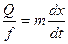 или u =mu. (1.13)
или u =mu. (1.13) или
или  (1.14)
(1.14)


