Плоскорадиальное движение. Приток к совершенной скважине, расположенной в центре кругового пласта
Примем следующие обозначения (рис.2.2): Если фильтрация происходит через всю цилиндрическую поверхность f =2 pr c h, то скважина называется гидродинамически совершенной по вскрытию. Наша задача определить расход жидкости, закон распределения давления, форму депрессионной поверхности, время движения частицы и форму индикаторной кривой. Вырежем мысленно элементарную радиальную струйку (см. рис. 2.2). Замечаем, что s = R к- r, a ds =- dr. С учетом этого закона Дарси в дифференциальной форме запишется как:
Но так как Q = fu =2 prhu, то
Рис.2.2. Схема плоскорадиального притока жидкости в пласте (приток к совершенной скважине) Н к — постоянный напор на круговом контуре питания; Н с — напор на забое скважины; Н — напор в любой точке пласта на расстоянии r от скважины; Р к, Р с, Р — приведенные давления на контуре питания, на забое и на расстоянии r соответственно.
Разделяя переменные и интегрируя в соответствующих пределах, получаем
откуда имеем:
Получили уравнения логарифмических кривых. Таким образом, пьезометрическая поверхность АВСД представляет собой поверхность вращения логарифмической кривой относительно оси скважины (см. рис. 2.2). Интегрируя уравнение (2.7) в пределах от Н с до Н и от r с до r, получим другое выражение для распределения давления (напора):
При r = r c имеем Н = Н с и Р = Р с. Тогда из (2.8) следует
Получили формулы Дюпюи для расхода. Подставляя (2.10) в (2.8), находим:
Таким образом, пьезометрическая поверхность или «воронка депрессии» (см. рис. 2.2) может быть построена по формулам (2.8), (2.9) и (2.11). Заметим, если пьезометрическая поверхность жидкости в пласте выше, чем поверхность земли, то скважина будет фонтанировать. При отсутствии отбора пьезометрическая поверхность занимает положение АД (см. рис. 2.2) и во всех точках пласта давление при этом одинаково. В случае отбора статический уровень в скважине понижается на величину а (см. рис. 2.2) и устанавливается так называемый динамический уровень. Формулу (2.10) можно записать в виде Q = КDР = К (Р к– Р c), (2.10') где
Здесь К принято называть коэффициентом продуктивности скважины. Размерность: Согласно (2.10') зависимость между Q и D Р является линейной и графически выражается прямой (рис. 2.3). В практике эта зависимость называется индикаторной диаграммой и снимается она при исследовании скважин методом пробных откачек, т. е. при установившихся отборах. Индикаторная диаграмма характеризует продуктивность скважины, режим фильтрации и помогает устанавливать режим работы скважины.
Рис.2.3. Индикаторная диаграмма "дебит-депрессия" при фильтрации несжимаемой жидкости по линейному закону Дарси
2.3. Время движения частицы жидкости, движущейся по радиусу от контура питания к скважине Истинная скорость движения в точке N (см. рис. 2.2) будет равна
Здесь принят знак (‑;), т. к. функция dr убывающая. Разделив переменные и проинтегрировав (2.13), получаем
При t =0 имеем r = R к, т. е.
Тогда
Получили формулу закона движения частицы. При r = r c получим время прохождения частицы от точки N до забоя скважины.
|

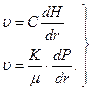 (2.5)
(2.5)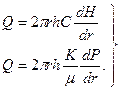 (2.6)
(2.6)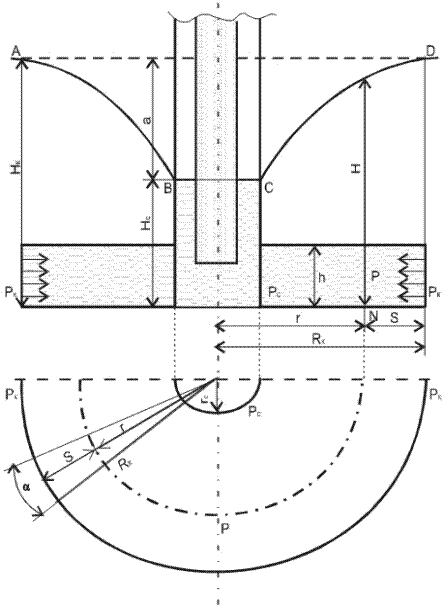
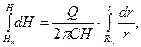 (2.7)
(2.7)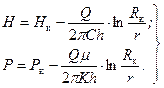 (2.8)
(2.8)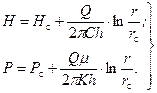 (2.9)
(2.9)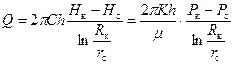 . (2.10)
. (2.10)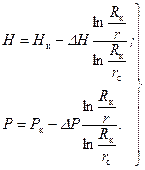 (2.11)
(2.11)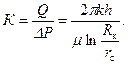 (2.12)
(2.12)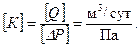 При D Р =1 Па имеем К=Q, т. е. коэффициент продуктивности выражает дебит на 1 Па перепада давления.
При D Р =1 Па имеем К=Q, т. е. коэффициент продуктивности выражает дебит на 1 Па перепада давления.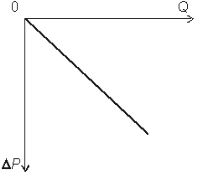
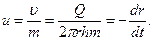 (2.13)
(2.13)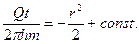 (2.14)
(2.14)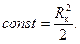 (2.15)
(2.15)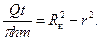 (2.16)
(2.16)


