Критических чисел Рейнольдса
Критические числа оказались в пределах 1£Reкр£1,4, т. е. в этой зоне происходит искривление прямой (линейность закона Дарси нарушается). Академик Павловский за линейный размер принял
и получил 7,5£Reкр£9. В.Н. Щелкачев, обработав данные Н.Н. Павловского, получил 1£Reкр£12 при
М.Д. Миллионщиков принял в качестве а=
где А и В –постоянные коэффициенты, определяемые из опытов; при малых числах Re первый член является доминирующим (В =0) и имеет место линейный закон фильтрации. При больших числах Re будем иметь l = В=сonst, т. е. квадратичный закон. Вопросам применимости закона Дарси посвящены также работы М. Маскета, А.И. Абдулвагабова, Г.Ф. Требина, Н.П. Лебединца и других исследователей. Заметим, что нарушение закона Дарси еще не означает нарушения ламинарности течения. Опыты Линдквиста и других исследователей показывают, что нарушение ламинарности происходит при числах Reгораздо больших, чем Reкp. Причиной нарушения закона Дарси является проявление роли сил инерции, а причиной нарушения ламинарности является проявление турбулентности потока при достаточно больших скоростях движения. 1.4.2. Нарушение линейного закона при малых скоростях. Экспериментальные исследования последних лет показали, что нарушение линейности закона фильтрации происходит и при малых скоростях. При этом отмечается, что движение некоторых пластовых жидкостей, обладающих реологическими свойствами (структурной вязкостью и начальным напряжением сдвига), начинается лишь при градиенте давления, превышающем некоторую критическую величину d, называемую предельным градиентом давления сдвига. В этом случае фильтрация не подчиняется закону Дарси и описывается так называемым обобщенным уравнением Дарси с предельным градиентом
Легко видеть, если d =0 (жидкость ньютоновская), то из (1.33) следует известный закон Дарси в векторной форме. Обобщенный закон Дарси можно записать в другой форме, например:
где h –коэффициент структурной вязкости жидкости как функция динамического напряжения сдвига t 0. В развернутом виде уравнение (1.34) представляется как
Связь между d и h (t 0) может быть установлена из уравнений(1.33) и (1.35). Тогда, оценивая второе слагаемое в (1.35), в некоторых случаях получим упрощенное выражение для обобщенного закона Дарси, т. е.
При таком законе краевые задачи теории фильтрации поддаются решению. Если принять h (t 0)= m, то из (1.36) или (1.34) следует закон Дарси для фильтрации обычной вязкой (ньютоновской) жидкости. Обобщенный закон Дарси свидетельствует об аналогии движения вязких и вязкопластичных жидкостей в капиллярах и пористой среде. 1.4.3. Обобщенная интерпретация законов фильтрации. Итак, движение жидкостей и газов в пористых средах, происходит как по линейному, так и по нелинейному законам фильтрации. При решении различных задач подземной гидродинамики для случаев нелинейной фильтрации за основу обычно берут формулу Дарси, в которой градиент давления возводится в некоторый показатель степени, или линейный закон фильтрации представляют двучленной формулой вида (1.32), одно из слагаемых которой также выражает закон Дарси. Существуют также и одночленные нестепенные формулы, выражающие нелинейный закон фильтрации, где вводится некоторый коэффициент фильтрационного сопротивления l как функция числа Рейнольдса Re. Существуют различные способы подхода к выводу формул, описывающих нелинейные законы фильтрации. Наиболее распространенными оказались способы, основанные на теории подобия и теории размерностей. Наиболее удачной характеристикой режима фильтрации считается параметр Дарси (Да), введенный В.Н. Щелкачевым (1946). Здесь мы не будем приводить и повторять те многочисленные формулы, которые описывают нелинейные законы фильтрации, а дадим обобщенную интерпретацию законов фильтрации, исходя из формулы (1.36), которую запишем в виде:
Мы ввели некоторый коэффициент l * как функцию скорости фильтрации, а также как функцию, зависящую от структуры пористой среды, пористости и т. д., т. е., другими словами, как функцию обобщенного критерия Рейнольдса Ясно, что формула(1.37) является обобщенным законом фильтрации. На самом деле, для линейного закона фильтрации должно быть l *=1 и из (1.37) следует линейный закон Дарси. Для нелинейного закона фильтрации l *>1. Таким образом, коэффициент l * показывает степень отклонения от линейного закона фильтрации. Если проинтегрировать уравнение (1.37), то получим
где F и L – площадь сечения и длина образца керна. Как видим, l * является обратной величиной параметра Дарси, т. е. представляет собой безразмерный параметр Лагранжа. Во многих исследованиях обработка экспериментальных результатов по фильтрации жидкостей производилась по формуле вида (1.38). Принятие заведомо квадратичного закона сопротивления от скорости фильтрации по аналогии с движением жидкостей в трубах привело к тому, что в диапазоне линейного закона фильтрации с увеличением скорости фильтрации коэффициент l уменьшается. Это вносит в закон Дарси излишнее усложнение. Величина коэффициента l, определенная на основе обработки экспериментальных данных по формуле (1.38), может меняться в огромном диапазоне: от 10 до 109. Попытка получить универсальную характеристику для всех образцов пористых сред, исходя из формулы (1.38), делалась многими авторами, но оказывалась безуспешной. Существенные достижения в этой области достигнуты А.И. Абдулва-габовым, выполнившим наиболее полные экспериментальные исследования по установлению верхней границы применимости закона Дарси. Однако диапазон изменения критического числа Re для различных образцов пористых сред оказался весьма широк. Здесь так же, как и в ранних исследованиях, экспериментальная обработка зависимости l =(Re) в логарифмических координатах дает единую прямую для разных сред в линейной области и разветвленную ветвь кривых в области нелинейной фильтрации. Впервые универсальную кривую в координатах Да, Некоторые обобщения аналогичных закономерностей (введжение параметра Лагранжа l * и обобщенного критерия Рейнольдса Rе*) для процессов изометрического движения газа, газированных и неньютоновских (глинистых растворов) жидкостей в трубах сделаны в работах [3, 4].
|

 (1.30)
(1.30)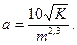
 (1.31)
(1.31)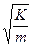 – так называемый масштаб породы и получил 0,022£Reкp£0,29. Е.М. Минский обработал результаты опытов американских авторов по двучленной формуле
– так называемый масштаб породы и получил 0,022£Reкp£0,29. Е.М. Минский обработал результаты опытов американских авторов по двучленной формуле , (1.32)
, (1.32)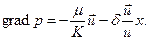 (1.33)
(1.33) ,(1.34)
,(1.34)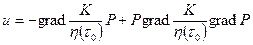 . (1.35)
. (1.35) (1.36)
(1.36) (1.37)
(1.37) .
. , (1.38)
, (1.38) ; c ' – коэффициент пропорциональности, характеризующий пористую среду и имеющий размерность L -1)удалось получить Н.П. Лебединцу [1] из экспериментальных данных Г.Ф. Требина. При этом параметр Да меняется, сравнительно с коэффициентом l, в очень узком диапазоне: от 1 до 0,05, что соответствует изменению параметра Лагранжа от 1 до 20. Более подробно границы применимости закона Дарси и его обобщение рассмотрены в работе [3].
; c ' – коэффициент пропорциональности, характеризующий пористую среду и имеющий размерность L -1)удалось получить Н.П. Лебединцу [1] из экспериментальных данных Г.Ф. Требина. При этом параметр Да меняется, сравнительно с коэффициентом l, в очень узком диапазоне: от 1 до 0,05, что соответствует изменению параметра Лагранжа от 1 до 20. Более подробно границы применимости закона Дарси и его обобщение рассмотрены в работе [3].


