Основные положения упругого режима
Как показали теоретические исследования и эксперименты, а также многолетняя практика разработки нефтегазоводоносных пластов, упругие свойства жидкостей и породы оказывают существенное влияние на показатели разработки залежей. Эти свойства необходимо учитывать при подсчете запасов нефти и газа, при проектировании разработки месторождений, а также в процессе их эксплуатации. Известно, что в пластовых условиях в жидкости (нефти) содержится газ как в свободном, так и в растворенном состоянии. Причем, если пластовое давление в процессе эксплуатации превышает давление насыщения жидкости газом, то весь пластовый газ находится в растворенном состоянии и к забоям скважин поступает однородная (однофазная) жидкость (нефть). В этом случае источником пластовой энергии является упругая деформация пласта и упругость насыщающей его жидкости, и режим пласта называется упругим. При этом в начальной стадии эксплуатации упругие свойства проявляются лишь в окрестности скважины и с течением времени происходит перераспределение давления вплоть до контура пласта. Если пласт является закрытым (например, выклинивается или ограничен непроницаемыми сбросами), то он работает на истощение и режим пласта называется замкнуто-упругим. В большинстве случаев источником энергии вытеснения нефти из пласта к забоям скважин является естественный или создаваемый напор контурными и подошвенными водами. В этом случае режим пласта характеризуется как упруго-водонапорный. Существует понятие и жесткого водонапорного режима, когда упругие силы проявляют себя весьма слабо. Теория упругого режима была начата работами И. Н. Стрижова, М. Маскета, Р. Шилсюида и У. Херста. Однако наиболее строго основы теории упругого режима были разработаны в нашей стране В. Н. Щелкачевым. Им были впервые учтены влияние объемной упругости пористой среды и ряда важных факторов на фильтрацию жидкостей и впервые решены фундаментальные задачи теории упругого режима для практических целей разработки нефтяных месторождений. Затем последовал ряд работ как советских, так и зарубежных ученых. Одними из важных параметров теории упругого режима являются коэффициенты объемной упругости жидкости (b ж)и пласта (b с). Количество жидкости, получаемое из пласта за счет упругих свойств (расширение жидкости и уменьшение порового пространства) при снижении пластового давления, принято называть упругим запасом пласта (D V), который, согласно В. Н. Щелкачеву, определяется формулами:
где b D P – изменение пластового давления, МПа. Коэффициенты объемной упругости имеют следующий порядок величин: для нефти bн =(7¸30)´10-4 1/МПа; для воды bв =(2,7¸5)´10-4 1/МПа; для сцементированных горных пород bс =(0,3¸2) ´10-4Мпа. Величина, обратная коэффициенту объемной упругости К=β;-1, называется модулем объемной упругости или модулем объемного сжатия. При пуске «возмущаюей скважины» возмущение передается по всей области пласта. Скорость перераспределения давления в пласте характеризуется величиной æ, называемой коэффициентом пьезопроводности, который выражается формулой
где m – коэффициент абсолютной вязкости, K – коэффициент проницаемости вдоль напластования. Размерность коэффициента пьезопроводности [ æ;]= L 2 T -1. Величины его заключены в интервале 0,1≤ При изучении неустановившихся процессов перераспределения давления в пласте удобно пользоваться безразмерными параметрами Фурье, введенными В.Н. Щелкачевым.
Как видим, параметры Фурье представляют собой «безразмерное время».
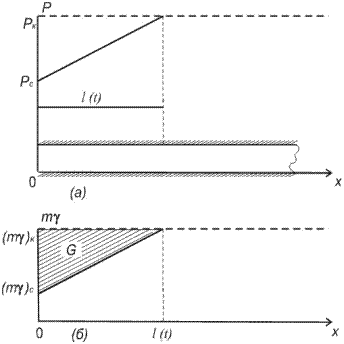
7.2 Решение одномерных задач методом последовательной смены стационарных состояний 7.2.1. Расчет притока к прямолинейной галерее. Рассмотрим полубесконечный пласт (рис. 7.1), где имеет место приток упругой жидкости к галерее. Пусть в сечении х =0 давление в пласте упало от начального давления P к до величины давления на галерее p с. Тогда точное решение задачи выражается интегралом вероятности [5]. Можно предложить наиболее простое, приближенное решение этой задачи. Пусть за время t зона пониженного давления распространилась на l (t) (см. pиc.7.1а).Будем считать, что в этой зоне распределение давления является стационарным [5]. На самом деле зона пониженного давления охватывает весь пласт и распределение давления не происходит по закону прямой линии, как для прямолинейного движения несжимаемой жидкости, т. е.
Таким образом, эпюра давления представляет собой прямую линию, перемещающуюся вдоль пласта с угловой точкой х=l (t), рис. 7.1б.Для точного решения эпюра давления угловой точки не имеет. В этом и состоит суть метода последовательной смены стационарных состояний. Выделим элемент пласта длиной dx и площадью поперечного сечения f= 1. Очевидно, элементарный вес в данном объеме составит mgdx×;1= тgdx, авес жидкости по длине l = l (t) на единицу площади выразится интегралом
Отобранное количество жидкости G из пласта за время t равно разности первоначального количества жидкости и остатка в пласте, т. е.
Рис.7.1.Схема к расчету неустановившегося притока сжимаемой
|

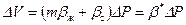 ;
;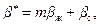
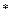 – коэффициент упругоемкости пласта, 1/МПа, показывающий, на какую часть первоначального объема изменяется объем жидкости в элементе при уменьшении давления на единицу;
– коэффициент упругоемкости пласта, 1/МПа, показывающий, на какую часть первоначального объема изменяется объем жидкости в элементе при уменьшении давления на единицу;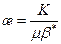 ,
,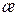 ≤5, где [ æ;]=м2/с.
≤5, где [ æ;]=м2/с.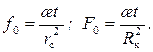
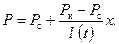 (7.1)
(7.1)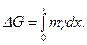
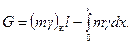 (7.2)
(7.2)