При вытеснении нефти водой
(по Чарному–Чен Чжун-Сяну)
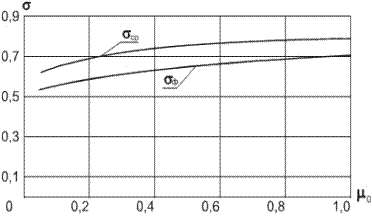
Рис.6.12.Зависимость насыщенности на фронте вытеснения и средней насыщенности от параметра m 0 =m в /m н для случая вытеснения нефти водой (по Чарному–Чен Чжун-Сяну) Результаты расчетов могут быть успешно использованы для практических целей: при расчетах безводного периода работы несовершенных скважин, при оценке степени извлечения нефти в удельном объеме дренирования и за период истощения, при совместном отборе нефти и воды, а также для оценки распределения насыщенности вдоль пласта при фильтрации двухфазной смеси и устранения многозначности функции f '1(s) путем введения скачка насыщенности (рис.6.13 и рис.6.13').
6.7.5. Скачки насыщенности. С помощью решения (6.22), зная положение точки с насыщенностью s в момент t =0, можно определить ее положение в любой момент времени t >0. Дифференцируя (6.22) по времени t находим:
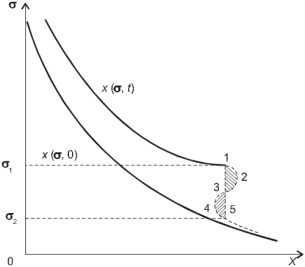
Нетрудно заметить, что выражение (6.70) представляет собой скорость распределения насыщенности. Вид кривых f (s) и f '(s) показан на рис. 6.6. Из графиков видно, что для одного и того же значения функции f '(s) существуют два значения насыщенности. Это говорит о многозначности s, что противоречит физическому смыслу. Чтобы избежать указанного парадокса, вводят понятие «скачка насыщенности» (рис. 6.13), который приводит к однозначности распределения насыщенности. Действительно, из графика (см. рис. 6.13), построенного по формуле (6.33), видно, что одной и той же точке пласта соответствуют три значения насыщенности (1, 3, 5), что физически невозможно. Вводя понятие скачка насыщенности из условия равенства площадей сегментов по обе стороны скачка (D S 1,2,3=D S 3,4,5), получим линию 1–3–5 (см. рис. 6.13), где насыщенность меняется скачком от s 2 до s 1. Заметим, что скачок насыщенности представляет собой понятие математическое, не имеющее места в реальных условиях. В действительности же существует конечная длина d (рис. 6.14), где значение насыщенности падает от s ф, до нуля перед фронтом вытеснения. Размер этой зоны (d) зависит от капиллярных свойств среды и по сравнению с «переходной зоной» – зоной смеси (1+2) очень мал. Часто в расчетах этой зоной пренебрегают (d =0) и рассматривают лишь переходную зону. Пусть жидкость (1) вытесняет жидкость (2) (см. рис. 6.14). Объем первой фазы в начальный момент (t =0) при s (х)= s =1 запишется интегралом
Рис. 6.14. Распределение насыщенности при вытеснении нефти водой
В момент времени t объем вторгшейся фазы (воды) в этой зоне выразится формулой
где х ф – координата фронта или скачка. За время t через границу х =0, оче видно, войдет объемное количество жидкости w t равное при S (x)= S =1
Принимая для простоты насыщенность нефтью переходной зоны в начальный момент s 2(х, 0)=1, что равнозначно s 1(х, 0)=0, из (6.73) получаем
а из (6.33) следует
или
Подставляя (6.76) в (6.74), находим
где
Здесь s 0 – насыщенность в сечении х =0. В нашем случае s 0=1. Согласно (6.28) имеем f (s)= f (1)=1,
или
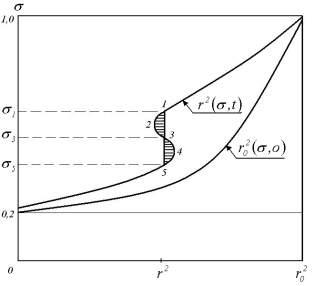
Из этого уравнения определяется фронтальная насыщенность. Средняя насыщенность в переходной зоне определится как частное от деления объема вторгшейся жидкости (воды) за время t на поровый объем mx ф, т. е. Учитывая (6.75), получаем формулу (6.68). Анализы показывают, что формулы (6.68) остаются справедливы и для плоскорадиальной двухфазной фильтрации. Для плоскорадиальной двухфазной фильтрации схема распределения насыщенности показана на рис.6.13' в соответствии с уравнением (6.33)'.
6.7.6. Понятие о трехфазной фильтрации. В реальных условиях часто приходится иметь дело с трехфазной фильтрацией (когда смесь состоит из трех компонентов, например, нефти, воды и свободного газа). Решение таких задач оказываются более сложными. Теорию фильтрации трехфазной смеси можно построить исходя из теории движения двухфазных жидкостей Бакли–Леверетта. Расходы каждой из фаз в смеси записываются как и для двухфазной системы
где
m – коэффициент абсолютной вязкости i -й фазы в смеси; S (x) – площадь фильтрации. К уравнениям движения следует добавить уравнения неразрывности
Так как s 1+ s 2+ s 3=1, (6.82) то в системе (6.81) независимых переменных только два. Справедливо также, что суммарный объемный расход является только функцией времни Q = Q 1+ Q 2+ Q 3= Q (t). (6.83) Далее расчеты ведут по следующей схеме. Из системы уравнений движения (6.80) и уравнений неразрывности (6.81) находятся газонефтяной и водоняфтяной факторы, а затем через них получают формулы для функций По экспериментальным данным для фиксированных значений насыщенности газом, давлений и физических параметров жидкостей строят зависимости
6.15. Зависимость K г/ K н от насыщенности s н при параметре s г
Рис. 6.16. Зависимость K в/ K н от насыщенности s н при параметре s г
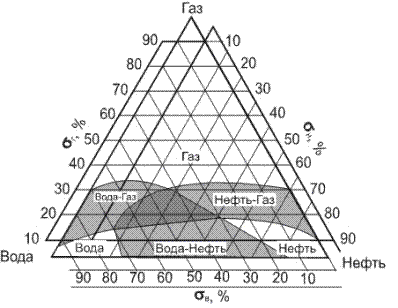
Пусть по промысловым данным значения отношений определены: Распределение насыщенности для трехкомпонентных систем хорошо иллюстируется треугольной диаграммой (рис. 6.17), на которой выделены области преобладания потоков различных фаз. Например, при газонасыщенности s г³0,35 поток состоит только из газа. При газонасыщенности s г=0,20 и водонасыщенности s в=0,50 будем иметь трехфазный поток (двойная штриховка) с нефтенасыщенностью s н=0,30. На диаграмме показаны также и области двухфазных потоков.
Рис. 6.17. Диаграмма для трехфазной фильтрации Подробное изложение теории трехфазной фильтрации приведено в монографиях [4, 5].
|

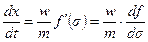 . (6.70)
. (6.70)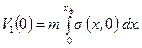 (6.71)
(6.71)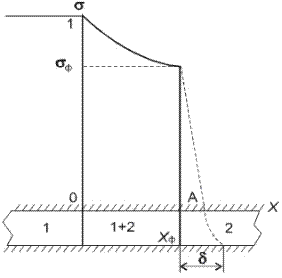
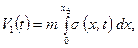 (6.72)
(6.72)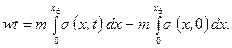 (6.73)
(6.73)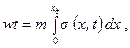 (6.74)
(6.74)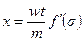 (6.75)
(6.75)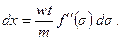 (6.76)
(6.76)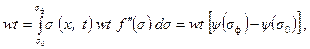 (6.77)
(6.77) (6.78)
(6.78)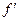 (1)=0. Тогда уравнение (6.77) упрощается и примет вид
(1)=0. Тогда уравнение (6.77) упрощается и примет вид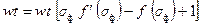
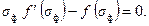 (6.79)
(6.79)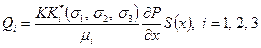 , (6.80)
, (6.80)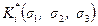 – относительные фазовые проницаемости как функции насыщенности, определяемые экспериментальным путем;
– относительные фазовые проницаемости как функции насыщенности, определяемые экспериментальным путем;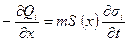 . (6.81)
. (6.81)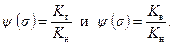 Таким образом, зная газонефтяной и водонефтяной факторы, по промысловым данным подсчитываются значения
Таким образом, зная газонефтяной и водонефтяной факторы, по промысловым данным подсчитываются значения 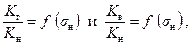 типовой вид которых представлен на рис.6. 15 и рис.6. 16.
типовой вид которых представлен на рис.6. 15 и рис.6. 16.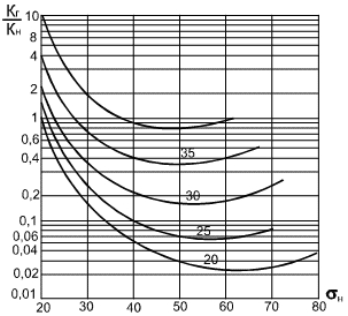

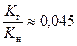 и
и 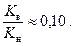 Тогда из графиков (см. рис. 6.15) находим: s г=0,20 и s н=0,45. Следовательно, насыщенность водой составляет s в=0,35.
Тогда из графиков (см. рис. 6.15) находим: s г=0,20 и s н=0,45. Следовательно, насыщенность водой составляет s в=0,35.