Кинематические условия на подвижной границе раздела. Характер движения водонефтяного контакта (ВНК) в наклонных пластах
В реальных условиях механизм движения границы раздела много сложнее, чем рассмотренный до этого. Рассмотрим наклонный пласт, где первоначальная граница горизонтальная (рис. 6.4). Пусть пласт вскрывается скважинами в нефтяной зоне. При отборе нефти водонефтяной контакт (ВНК) будет перемещаться вверх. Если площадь ВНК сравнительно мала, то перемещение границы раздела можно считать равномерным, т. е. подвижная поверхность остается параллельной первоначальному положению ВНК. При достаточно большой площади ВНК картина движения искажается, в большинстве случаев происходит опережение в движении границы раздела по подошве пласта, т. е. имеет место пространственное движение. Точного решения о пространственном движении границы раздела не имеется. Основная трудность такого решения заключается в том, что на границе происходит преломление линий тока. Рассмотрим следующую схему (рис. 6.5). Возьмем на границе раздела произвольную точку М и проведем через нее касательную
Из (6.13) видно, что
откуда видно, что Приближенные методы решения задач пространственного движения границы раздела заключаются в следующем. 1. Полагают, что вязкость и плотность воды и нефти одинаковы, и решают задачу для одножидкостной системы с последующим введением поправок па различие в вязкостях и плотностях жидкостей. При таких допущениях линии тока и траектории частиц совпадают, а потенциал и скорость легко рассчитываются. 2. Полагают послойное движение частиц (метод В.Н. Щелкачева), т. е. движение, предполагается параллельным кровле или подошве. По этой схеме можно оценить опережение частиц по подошве пласта. 3. Рассматривают пласт однородно-анизотропный, где К х и К у – проницаемости в двух взаимно перпендикулярных плоскостях. Пределы истинного движения устанавливаются краевыми условиями: К у=0 и К у=¥. По следний случай соответствует гидравлической теории безнапорного движения о гидростатическом распределении давления в каждом поперечном сечении потока. Рассмотрим вопрос об устойчивости границы раздела. Если частица вытесняющей жидкости (воды), попавшая в область, занятую вытесняемой жидкостью (нефти), замедляет свое дальнейшее движение, такое движение называется устойчивым. При ускорении последующего движения процесс называется неустойчивым. Для вытесняющей и вытесняемой жидкостей (воды и нефти) закон Дарси в общем виде записывается следующими формулами:
Если первая жидкость (вода) проникла во вторую (нефть), то для первой жидкости закон Дарси записывается в виде
Тогда разность скоростей D w =(w 1)2 – w 2 выразится формулой
Проникновение первой жидкости в зону движения второй происходит вдоль кровли или по подошве. Тогда значение Если D w £0, то движение устойчиво; при D w >0 движение неустойчиво. Движение всегда устойчиво при малых скоростях и когда g1>g2, a >0. Чарным И.А. показано [5], что схема движения K y=¥ всегда дает неустойчивое движение.
|

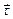 и нормаль
и нормаль 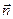 . Очевидно, нормальные составляющие скорости движения воды и нефти в точке М будут равны, т. е. (Wn)в=(Wn)н, т. к. в силу неразрывности потока элементарные расходы воды и нефти через сечение dw равны. Касательные, составляющие скорости обеих жидкостей, согласно закону Дарси записываются в виде
. Очевидно, нормальные составляющие скорости движения воды и нефти в точке М будут равны, т. е. (Wn)в=(Wn)н, т. к. в силу неразрывности потока элементарные расходы воды и нефти через сечение dw равны. Касательные, составляющие скорости обеих жидкостей, согласно закону Дарси записываются в виде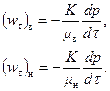 (6.13)
(6.13)
 , так как
, так как  . Причем где вязкость меньше, там тангенциальная скорость больше. Векторы скорости для частицы воды и нефти записываются в форме (рис. 6.5)
. Причем где вязкость меньше, там тангенциальная скорость больше. Векторы скорости для частицы воды и нефти записываются в форме (рис. 6.5) (6.14)
(6.14) Таким образом, на границе раздела скорость частицы претерпевает разрыв и линия тока (АМВ) преломляется. Линии тока не будут преломляться в двух случаях: при прямолинейном и плоскорадиальном движениях, уже нами рассмотренных. Поэтому здесь и возможны точные решения задачи о продвижении границы раздела. В этих случаях касательные, составляющие скорости фильтрации, равны нулю (wt =0).
Таким образом, на границе раздела скорость частицы претерпевает разрыв и линия тока (АМВ) преломляется. Линии тока не будут преломляться в двух случаях: при прямолинейном и плоскорадиальном движениях, уже нами рассмотренных. Поэтому здесь и возможны точные решения задачи о продвижении границы раздела. В этих случаях касательные, составляющие скорости фильтрации, равны нулю (wt =0). (6.15)
(6.15)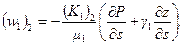 (6.16)
(6.16) (6.17)
(6.17)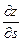 представляет собой sin a, где a — угол наклона пласта к горизонту (рис. 6.5). Проницаемость (K 1)2 — это проницаемость переходной зоны, которая много меньше K 2. В первом приближении можно принять (K 1)2» K 2. Скорость w 2 определяют по дебиту скважины. Следовательно, можно оценить D w.
представляет собой sin a, где a — угол наклона пласта к горизонту (рис. 6.5). Проницаемость (K 1)2 — это проницаемость переходной зоны, которая много меньше K 2. В первом приближении можно принять (K 1)2» K 2. Скорость w 2 определяют по дебиту скважины. Следовательно, можно оценить D w.


