Безнапорной фильтрации через прямоугольную перемычку
Горизонтальная компонента скорости фильтрации
Эта компонента предполагается постоянной вдоль вертикали. Вертикальная компонента по условию равна нулю. Расход на единицу ширины потока f =1 запишется выражением
Итак мы видим, что отличительным признаком безнапорного движения является линейная зависимость потенциала или функции Н на свободной поверхности от вертикальной координаты Z.
5.2. Гидравлическая теория безнапорного движения через прямоугольную перемычку на горизонтальном основании Определим из (5.3) уравнение свободной поверхности. Разделяя переменные и интегрируя, получим
Используя граничные условия (см. рис. 5.1)
находим
Решая совместно (5.6) и (5.7), находим расход
Подставляя (5.6) в (5.4) и учитывая (5.8), находим
Получили уравнение параболы. Таким образом, поверхность депрессии является параболой (линия АС, рис 5.1). В действительности формула (5.9) несправедлива. Это видно из следующих соображений. При Р 2=0 у выхода в нижний бьеф (х = l) из формулы (5.9) получаем, что h =0. Это приводит к бесконечной скорости фильтрации Формула Дюпюи (5.8), хотя и выведена из допущений гидравлической теории, является строго точной. Строгое доказательство ее дано И.А. Чарным [5].
5.3. Гидравлическая теория безнапорного притока к совершенной скважине Рассмотрим приток к совершенной скважине. Все обозначения даны на рис. 5.2. Движение считаем установившимся, т. е. Q и h = h (r) от времени не зависят. Скважину считаем стоком, следовательно, дебит будет положительным. Скорость фильтрации по закону Дарси
Если f =2 prh — площадь фильтрации при плоскорадиальном притоке, то дебит скважины выразится формулой
Знак минус здесь не ставим, так как мы рассматриваем скважину сток, а функция h = h (r) является возрастающей функцией расстояния. Разделяя переменные в уравнении (5.11) и интегрируя, получаем
Из граничного условия h = H к при r = R к находим
Подставляя (5.13) в (5.12), найдем уравнение свободной поверхности (АСС ' A ', рис. 5.2). Используя второе граничное условие h = H c при r = r c и выражение (5.13), из (5.12) получаем формулу Дюпюи
Формула (5.14), как и формула (5.8), является строго точной.
5.4. Дифференциальные уравнения гидравлической теории нестационарной безнапорной фильтрации Согласно гидравлической теории безнапорного движения считается, что напор Н = Н (х, у, z, t) является постоянной величиной вдоль каждой вертикали, а горизонтальные проекции скорости фильтрации u, u равномерно распределены вдоль каждой вертикали. Тогда напор равен глубине потока (Н=h) и компоненты скорости запишутся в следующем виде:
Расходы потока на единицу ширины в направлениях х и у соответственно будут равны:
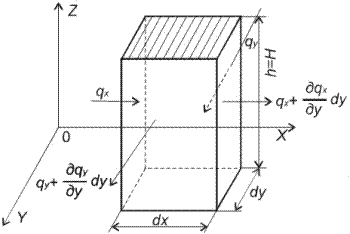
Составим уравнение неразрывности для нестационарного грунтового потока. Выделим элемент грунта высотой Н=h и площадью сечения dxdy (рис. 5.4). За время dt в параллелепипед поступает
Вытекает за то же время
Рис. 5.4. Схема к выводу уравнения гидравлической теории
Следовательно, накопленный объем за время dt составит
Этот объем идет на повышение высоты Н, которая за время dt меняется на величину
Приравнивая (5.17) и (5.18), находим
Подставляя значение q x и q y из (5.16) в (5.19), получим
или
Получили дифференциальное уравнение гидравлической теории нестационарного безнапорного потока Буссинеска. Как видим, уравнение это нелинейное параболического типа в частных производных. В общем случае точного решения не имеет. Точные решения для частных случаев имеются у П.Я. Полубариновой-Кочиной. Одним из методов приближенного решения подобных уравнений является метод линеаризации Л.С. Лейбензона. Л.С. Лейбензон указал замечательное сходство уравнения (5.21) с дифференциальным уравнением неустановившегося движения газа в пористой среде. В дальнейшем мы рассмотрим эту аналогию.
|

 (5.2)
(5.2) (5.3)
(5.3) (5.4)
(5.4)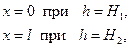 (5.5)
(5.5) (5.6)
(5.6) (5.7)
(5.7) (5.8)
(5.8)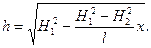 (5.9)
(5.9)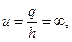 что невозможно. Поэтому необходимо, чтобы выполнялось условие hx = l > H 2, т. е. должен существовать промежуток высачивания.
что невозможно. Поэтому необходимо, чтобы выполнялось условие hx = l > H 2, т. е. должен существовать промежуток высачивания. (5.10)
(5.10)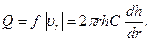 (5.11)
(5.11)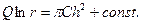 (5.12)
(5.12)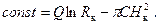 (5.13)
(5.13) (5.14)
(5.14) (5.15)
(5.15) (5.16)
(5.16)
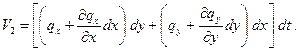
 (5.17)
(5.17)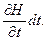 Учитывая пористость т, изменение объема можно записать еще в таком виде
Учитывая пористость т, изменение объема можно записать еще в таком виде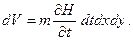 (5.18)
(5.18)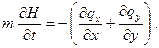 (5.19)
(5.19) (5.20)
(5.20)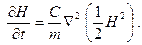 (5.21)
(5.21)


